
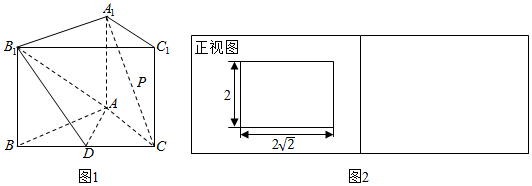
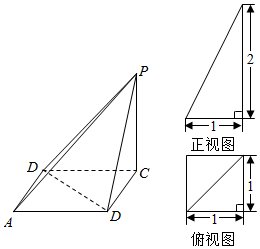
分析 (Ⅰ)(图2)给出了该三棱柱三视图中的正视图,根据直观图可得侧视图;
(Ⅱ)求连接A1C交A1C于A1C点,连接A1C,则A1C为A1C的中点,证明A1C∥A1C,即可证明A1C∥平面AB1D;
(Ⅲ)求出点P到平面AB1D的距离等于点C到平面AB1D的距离,利用等体积转化,即可求三棱锥P-AB1D的体积.
解答 解:(Ⅰ)该三棱柱的左视图如下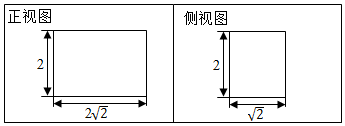 …(3分)
…(3分)
证明:(Ⅱ)连接A1C交A1C于A1C点,连接A1C,则A1C为A1C的中点.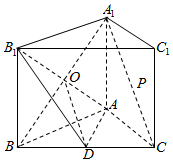
又∵A1C为A1C的中点,
∴A1C是A1C的中位线.
∴A1C∥A1C.…(5分)
∵AB1D平面AB1D,AB1D平面AB1D,
∴A1C∥平面AB1D.…(7分)
解:(Ⅲ)∵AA1⊥底面ABC,且CC1=AB=AC=2,∠BAC=90°.
∴AD⊥BC,且$AD=\sqrt{2},DC=\sqrt{2}$,故${S_{△ACD}}=\frac{1}{2}AD•DC=1$.…(8分)
又∵点P是线段A1C上的动点,由(Ⅱ)可知A1C∥平面AB1D,
故点P到平面AB1D的距离等于点C到平面AB1D的距离.…(9分)
∴${V_{P-A{B_1}D}}={V_{C-A{B_1}D}}={V_{{B_1}-ACD}}$.…(11分)
又∵BB1⊥面ABC,
∴$\frac{1}{3}{S_{△ACD}}•B{B_1}$═$\frac{1}{3}{S_{△ACD}}•B{B_1}$=$\frac{1}{3}×1×2$=$\frac{2}{3}$.
即三棱锥P-AB1D的体积为$\frac{2}{3}$.…(12分)
点评 本题考查的是三视图,考查线面平行的判定,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{5}$ | D. | $±\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
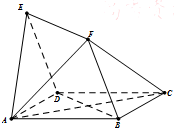 (文)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(文)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com