
分析 (Ⅰ)设圆的标准方程,利用待定系数法求解即可;
(Ⅱ)直线转化为点斜式,得出过定点M(2,1),显然点M在圆内,利用数形结合可知当直线L与CM垂直时,弦|AB|最小,求解即可.
解答 解:(Ⅰ)设圆的方程为(x-a)2+(y-b)2=r2,
∴a+b-3=0,
(1-a)2+(4-b)2=r2,
解得:a=1,b=2,r=2,
∴圆的方程为(x-1)2+(y-2)2=4,
(Ⅱ)直线L的方程可化为y-1=k(x-2),
∴过定点M(2,1),显然点M在圆内,
∴当直线L与CM垂直时,弦|AB|最小,
∵kcm=-1,
∴k=1,
∴L的方程为x-y-1=0.
∵|CM|=$\sqrt{2}$,r=2,
∴|AB|=2$\sqrt{2}$.
点评 考查了圆方程的求解和数形结合的应用,难点是对直线方程横过圆内定点的理解和应用.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
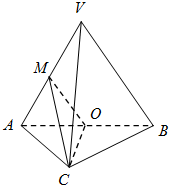 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com