
分析 (1)运用分析法证明.要证原不等式成立,可移项两边平方,化简整理,即可得证;
(2)要证原不等式成立,可分子常数化,运用不等式的性质和三角形的三边的关系,即可得证.
解答 证明:(1)运用分析法证明.要证原不等式成立,
只需证$\sqrt{a+5}$+$\sqrt{a+4}$>$\sqrt{a+6}$+$\sqrt{a+3}$,
两边平方即为2a+9+2$\sqrt{a+5}$•$\sqrt{a+4}$>2a+9+2$\sqrt{a+6}$•$\sqrt{a+3}$,
即有(a+5)(a+4)>(a+6)(a+3),即a2+9a+20>a2+9a+18,
20>18,显然成立,故原不等式成立;
(2)要证$\frac{a+b}{1+a+b}>\frac{c}{1+c}$成立,
只需证$1-\frac{1}{1+a+b}>1-\frac{1}{1+c}$,
只需证$-\frac{1}{1+a+b}>-\frac{1}{1+c}$,
只需证$\frac{1}{1+a+b}<\frac{1}{1+c}$,
只需证1+c<1+a+b,
只需证c<a+b,
由a,b,c是△ABC的三条边,
可得c<a+b成立,原不等式成立.
点评 本题考查不等式的证明,注意运用分析法证明,结合不等式的性质和三角形的三边关系,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 从匀速传递的产品生产流水线上,质检员每5分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样 | |
| B. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有${x^{\frac{1}{2}}}<{x^{\frac{1}{3}}}$,则 p∨(¬q)是真命题 | |
| C. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| D. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
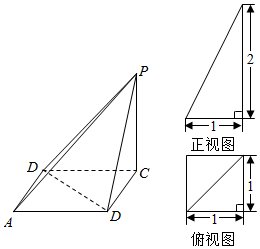
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
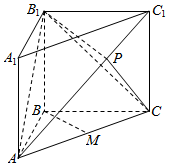 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AAl=2,∠ABC=120°,点P在线段AC1上,且AP=2PCl,M为线段AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AAl=2,∠ABC=120°,点P在线段AC1上,且AP=2PCl,M为线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com