
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.分析 (1)取A1B的中点F,连结EF,FD.则可证明四边形EFDC1是平行四边形,故而C1E∥DF,得出结论;
(2)证出A1B1⊥平面AA1C1C,则V${\;}_{{C}_{1}-{A}_{1}BD}$=V${\;}_{B-{A}_{1}{C}_{1}D}$=V${\;}_{{B}_{1}-{A}_{1}{C}_{1}D}$=$\frac{1}{3}{S}_{△{A}_{1}{C}_{1}D}•{A}_{1}{B}_{1}$.
解答 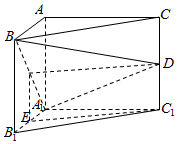 证明:(1)取A1B的中点F,连结EF,FD.
证明:(1)取A1B的中点F,连结EF,FD.
∵E,F是A1B1,A1B的中点,
∴EF$\stackrel{∥}{=}$$\frac{1}{2}$BB1,
又BB1$\stackrel{∥}{=}$CC1,D是CC1的中点,
∴EF$\stackrel{∥}{=}$C1D,
∴四边形EFDC1是平行四边形,
∴C1E∥DF,又DF?平面A1BD,C1E?平面A1BD,
∴C1E∥平面A1BD.
解:(2)∵AA1⊥平面A1B1C1,A1B1?平面A1B1C1,
∴AA1⊥A1B1,
∵∠B1A1C1=90°,
∴A1B1⊥A1C1,
又AA1?平面AA1C1C,A1C1?平面AA1C1C,AA1∩A1C1=A1,
∴A1B1⊥平面AA1C1C,
∵AA1∥BB1,
∴V${\;}_{{C}_{1}-{A}_{1}BD}$=V${\;}_{B-{A}_{1}{C}_{1}D}$=V${\;}_{{B}_{1}-{A}_{1}{C}_{1}D}$=$\frac{1}{3}{S}_{△{A}_{1}{C}_{1}D}•{A}_{1}{B}_{1}$=$\frac{1}{3}×\frac{1}{2}×2×1×1$=$\frac{1}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
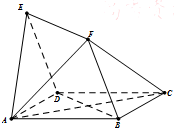 (文)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(文)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
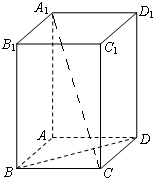 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99.9%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99.9%以上的把握认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{16}$,0) | B. | (0,$\frac{1}{16}$) | C. | ($\frac{1}{2}$,0) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com