
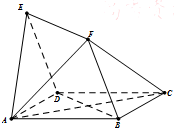
 (文)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(文)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.分析 (1)设AC,BD交于点O,连结OF,由三线合一可得FO⊥AC,由菱形性质得AC⊥BD,故而AC⊥平面BDEF;
(2)取AE,AF的中点M,N,连结DM,MN,ON,可证四边形ODMN是平行四边形,故而ON∥DM,又由中位线得力得FC∥ON,于是FC∥DM,从而FC∥平面EAD;
(3)由题意可得△ABD,△BDF,△BCD是边长为1的等边三角形,于是FO⊥BD,又FO⊥AC,得出FO⊥平面ABCD,于是VE-BCD=VF-BCD=$\frac{1}{3}{S}_{△BCD}•FO$.
解答 证明:(1)连结DF,设AC∩BD=O,连结OF.
∵四边形ABCD是菱形,
∴AC⊥BD,O是AC,BD的中点,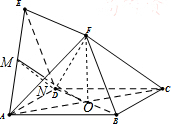
∵FA=FC,
∴FO⊥AC,
又∵DB?平面BDEF,FO?平面BDEF,DB∩FO=O,
∴AC⊥平面BDEF.
(2)取AE,AF的中点M,N,连结DM,MN,ON,
∵MN是△AEF的中位线,
∴MN$\stackrel{∥}{=}$$\frac{1}{2}EF$,
∵四边形BDEF是菱形,O是BD的中点,
∴OD$\stackrel{∥}{=}$$\frac{1}{2}EF$,
∴四边形ODMN是平行四边形,
∴ON∥DM,
∵ON是△AFC的中位线,
∴ON∥FC,
FC∥DM,又DM?平面EAD,FC?平面EAD,
∴FC∥平面EAD.
解:(3)∵四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AD=1,
∴△ABD,△BDF,△BCD是边长为1的等边三角形,
∴FO⊥BD,FO=$\frac{\sqrt{3}}{2}$,S△BCD=$\frac{1}{2}×1×1×sin60°$=$\frac{\sqrt{3}}{4}$.
又FO⊥AC,BD?平面ABCD,AC?平面ABCD,AC∩BD=O,
∴FO⊥平面ABCD.
∴VE-BCD=VF-BCD=$\frac{1}{3}{S}_{△BCD}•FO$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{\sqrt{3}}{2}$=$\frac{1}{8}$.
点评 本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
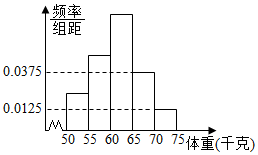 为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
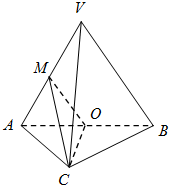 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
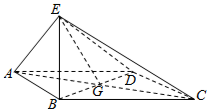 如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,
如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
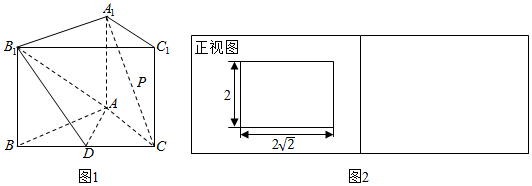
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com