

分析 (1)根据VB-AEF=VA-BEF列方程解出棱锥的高;
(2)棱锥的表面积为正方形的面积;
(3)建立空间坐标系,求出平面MNE的法向量$\overrightarrow{n}$,利用$\overrightarrow{n}$与$\overrightarrow{BE}$的夹角求出线面角.
解答 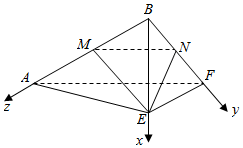 解:(1)∵AB⊥BE,AB⊥BF,BE,BF?平面BEF,BE∩BF=B,
解:(1)∵AB⊥BE,AB⊥BF,BE,BF?平面BEF,BE∩BF=B,
∴AB⊥平面BEF,
∴VA-BEF=$\frac{1}{3}{S}_{△BEF}•AB$=$\frac{1}{3}×\frac{1}{2}×2×2×4$=$\frac{8}{3}$.
设点B到面AEF的距离为h,
则VB-AEF=$\frac{1}{3}{S}_{△AEF}•h$.
∵S△AEF=S正方形ABCD-S△ABE-S△ADF-S△CEF=16-4-4-2=6.
VA-BEF=VB-AEF,
∴$\frac{1}{3}×6h=\frac{8}{3}$,
解得h=$\frac{4}{3}$cm.
即点B到面AEF的距离为$\frac{4}{3}$cm.
(2)∵几何体B-AEF的展开图是正方形ABCD
∴几何体B-AEF的表面积S=S正方形ABCD=16cm2.
(3)由(1)可知AB⊥平面BEF,同理可证BE⊥平面ABF,
∴BA,BE,BF两两垂直.
以B为坐标原点,建立如图所示的空间坐标系,
则B(0,0,0),E(2,0,0),M(0,0,2),N(0,1,0),
∴$\overrightarrow{BE}$=(2,0,0),$\overrightarrow{ME}$=(2,0,-2),$\overrightarrow{MN}$=(0,1,-2).
设平面MNE的法向量$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{n}⊥\overrightarrow{ME}$,$\overrightarrow{n}⊥\overrightarrow{MN}$.
∴$\left\{\begin{array}{l}{2x-2z=0}\\{y-2z=0}\end{array}\right.$,令z=1得$\overrightarrow{n}$=(1,2,1).
∴|$\overrightarrow{n}$|=$\sqrt{6}$,|$\overrightarrow{BE}$|=2,$\overrightarrow{n}•\overrightarrow{BE}$=2,
∴cos<$\overrightarrow{n},\overrightarrow{BE}$>=$\frac{\overrightarrow{n}•\overrightarrow{BE}}{|\overrightarrow{n}||\overrightarrow{BE}|}$=$\frac{\sqrt{6}}{6}$.
∴直线BE与面MNE所成角的余弦值为sin<$\overrightarrow{n}$,$\overrightarrow{BE}$>=$\sqrt{1-(\frac{\sqrt{6}}{6})^{2}}$=$\frac{\sqrt{30}}{6}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,空间角的计算,当空间角不方便作出时多采用向量法求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 平均车速超过 100km/h人数 | 平均车速不超过 100km/h人数 | 合计 | |
| 男性驾驶员人数 | 40 | 15 | 55 |
| 女性驾驶员人数 | 20 | 25 | 45 |
| 合计 | 60 | 40 | 100 |
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
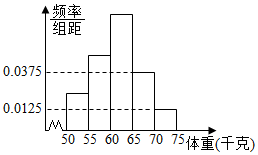 为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
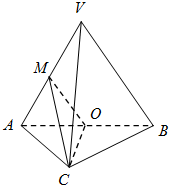 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
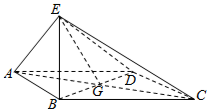 如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,
如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{15}$ | B. | $\frac{64π}{15}$ | C. | $\frac{15π}{4}$ | D. | $\frac{15π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com