练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．设i为虚数单位，n为正整数．试用数学归纳法证明（cosx+isinx）n=cosnx+isinnx．

    分析 利用数学归纳法即可证明．

    解答 解：①当n=1时，左边=cosx+isinx=右边，此时等式成立；
    ②假设当n=k时，等式成立，即（cosx+isinx）k=coskx+isinkx．
    则当n=k+1时，（cosx+isinx）k+1=（cosx+isinx）k（cosx+sinx）
    =（coskx+isinkx）（cosx+isinx）=coskxcosx-sinkxsinx+（coskxsinx+sinkxcosx）i
    =cos[（k+1）x]+isin[（k+1）x]，
    ∴当n=k+1时，等式成立．
    由①②得，（cosx+isinx）n=cosnx+isinnx．

    点评 本题考查了数学归纳法和三角函数的两角和差的正弦余弦公式，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知函数$f（x）=2sin（2x+\frac{π}{6}）+a+1$．
    （1）若$x∈[{0，\frac{π}{2}}]$且a=1时，求f（x）的最大值和最小值．
    （2）若x∈[0，π]且a=-1时，方程f（x）=b有两个不相等的实数根x1、x2，求b的取值范围及x1+x2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．把病人送到医院看病的过程用框图表示，则此框图称为（　　）
    A．工序流程图B．程序流程图C．组织流程图D．程序步骤图

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

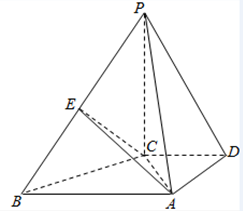    13．如图，在四棱锥P-ABCD中，PC⊥底面ABCD，底面ABCD是梯形，AB⊥AD，AB∥CD，AB=2，AD=CD=1，E是线段PB的中点．
    （1）证明：AC⊥平面PBC；
    （2）若点P到平面ACE的距离为$\frac{\sqrt{6}}{3}$，求三棱椎P-ACD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．如图在三棱柱ABC-A1B1C1中，侧面AA1C1C是矩形，且侧面AA1C1C⊥底面AA1B1B，M是AB的中点，若AA1=2，AC=1，∠A1AB=60°，CB1⊥A1B．
    （1）求证：AC1∥平面CMB1；
    （2）求三棱锥M-CC1B1的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知点P（tanα，cosα）在第三象限，则角α的终边在（　　）
    A．第四象限B．第三象限C．第二象限D．第一象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，O坐标原点，以OF直径的圆与双曲线的一条渐近线相交于O，A两点，且|OA|=2|AF|，则双曲线的离心率等于（　　）
    A．$\sqrt{3}$B．$\sqrt{5}$C．$\frac{3}{2}$D．$\frac{\sqrt{5}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．下列框图中是流程图的是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知定义在（0，+∞）上的单调函数f（x），对?x∈（0，+∞），都有f[f（x）-log2x]=3，则方程f（x）-f′（x）=2的解所在的区间是（　　）
    A．（0，$\frac{1}{2}$）B．（1，2）C．（$\frac{1}{2}$，1）D．（2，3）

    查看答案和解析>>

    同步练习册答案