练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知等差数列的前项和为，并且，，数列满足：，，记数列的前项和为．

    （1）求数列的通项公式及前项和公式；

    （2）求数列的通项公式及前项和公式；

    （3）记集合，若的子集个数为16，求实数的取值范围．

    【答案】（1）（2）（3）

    【解析】

    试题（1）数列是等差数列，可把已知用表示出来，列出方程组，解出，从而得到通项公式和胶项和；（2）由已知得，这是数列前后项的比值，因此可用连乘法求得通项，即，从而有，它可看作是一个等差数列和一个等比数列的乘积，因此其前项和用乘公比错位相减法求得；（3）由（1）（2）求得，不等式恒成立，即恒成立，只要求得的最小值即可，先求出前面几项，观察归纳猜想出单调性并给出证明（可用证明数列的单调性），从而可求得最小值，得范围．

    试题解析：（1）设数列的公差为，由题意得

    （2）由题意得

    叠乘得

    由题意得①

    ②

    ②-①得：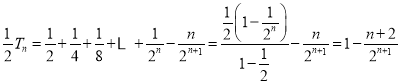

    （3）由上面可得令

    则

    下面研究数列的单调性，

    时，即单调递减.

    所以不等式解的个数为4，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2＋(x－1)|x－a|.

    (1)若a＝－1，解方程f(x)＝1；

    (2)若函数f(x)在R上单调递增，求实数a的取值范围；

    (3)是否存在实数a，使不等式f(x)≥2x－3对任意x∈R恒成立？若存在，求出a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数由方程到确定，对于函数给出下列命题：

    ①对任意，都有恒成立：

    ②，使得且同时成立；

    ③对于任意恒成立；

    ④对任意，，

    都有恒成立.其中正确的命题共有( )

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（理）已知数列满足（），首项．

    （1）求数列的通项公式；

    （2）求数列的前项和；

    （3）数列满足，记数列的前项和为，是△ABC的内角，若对于任意恒成立，求角的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义在上的函数，若函数满足：①在区间上单调递减；②存在常数p，使其值域为，则称函数为的“渐近函数”；

    （1）证明：函数是函数的渐近函数，并求此时实数p的值；

    （2）若函数，证明：当时，不是的渐近函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业参加项目生产的工人为人，平均每人每年创造利润万元.根据现实的需要，从项目中调出人参与项目的售后服务工作，每人每年可以创造利润万元（），项目余下的工人每人每年创造利图需要提高

    （1）若要保证项目余下的工人创造的年总利润不低于原来名工人创造的年总利润，则最多调出多少人参加项目从事售后服务工作？

    （2）在（1）的条件下，当从项目调出的人数不能超过总人数的时，才能使得项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某部影片的盈利额（即影片的票房收入与固定成本之差）记为,观影人数记为,其函数图象如图（1）所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图（2）、图（3）中的实线分别为调整后与的函数图象.

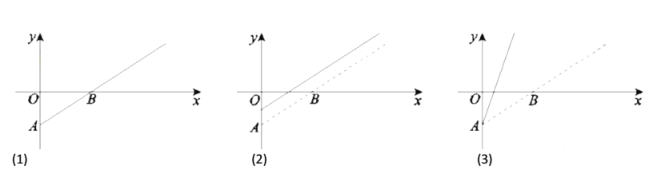
    给出下列四种说法:

    ①图（2）对应的方案是:提高票价,并提高成本;

    ②图（2）对应的方案是:保持票价不变,并降低成本;

    ③图（3）对应的方案是:提高票价,并保持成本不变;

    ④图（3）对应的方案是:提高票价,并降低成本.

    其中,正确的说法是____________.（填写所有正确说法的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知,数列的前项和为,且.

    (1)求证:数列是等比数列,并求出通项公式;

    (2)对于任意(其中,,均为正整数),若和的所有乘积的和记为,试求的值;

    (3)设,,若数列的前项和为,是否存在这样的实数,使得对于所有的都有成立,若存在,求出的取值范围;若不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案