
分析 把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.
解答 解:不等式|x+1|+|2x-1|<3等价于$\left\{\begin{array}{l}{x<-1}\\{-x-1+1-2x<3}\end{array}\right.$①,或$\left\{\begin{array}{l}{-1≤x<\frac{1}{2}}\\{x+1+1-2x<3}\end{array}\right.$②,或$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{x+1+2x-1<3}\end{array}\right.$③.
解①求得x∈∅,解②求得-1<x<$\frac{1}{2}$,解③求得$\frac{1}{2}$≤x<1,
综合可得,原不等式的解集为(-1,1),
故答案为:(-1,1).
点评 本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,属于基础题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
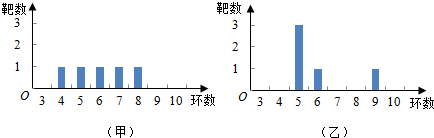
| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com