练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设数列{an}满足a1＋2a2＝3，且对任意的n∈N*，点列{Pn(n，an)}恒满足PnPn＋1＝(1,2)，则数列{an}的前n项和Sn为(　　)

    A．n(n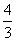－)                                                 B．n(n－)

    C．n(n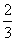－)                                                 D．n(n－)


    A

    [解析]　设Pn＋1(n＋1，an＋1)，则PnPn＋1＝(1，an＋1－an)＝(1,2)，即an＋1－an＝2，所以数列{an}是以2为公差的等差数列．又a1＋2a2＝3，所以a1＝－，所以Sn＝n(n－)，选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知A、B、C是圆O：x2＋y2＝r2上三点，且等于(　　)

    A．0　 　 　　B.　　 　C.　　　D．－

    查看答案和解析>>

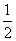    科目：高中数学 来源： 题型：


    设F1、F2为椭圆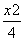＋y2＝1的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点，当四边形PF1QF2面积最大时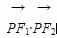，的值等于(　　)

    A．0　　　　B．2　　　　C．4　　　　D．－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}的通项公式an＝2n·sin，前n项和为Sn，则S2013＝(　　)

    A．1007                                                        B．－1007

    C．2013                                                        D．－2013

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列2008,2009,1，－2008，－2009，…这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2014项之和S2014等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于数列{an}，定义数列{an＋1－an}为数列{an}的“差数列”，若a1＝2，{an}的“差数列”的通项为2n，则数列{an}的前n项和Sn＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在等差数列{an}中，已知a4＋a8＝16，则a2＋a10＝(　　)

    A．12　 　　B．16　 　　C．20　 　　D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知{an}是等差数列，Sn为其前n项和，若S21＝S4000，O为坐标原点，点P(1，an)，Q(2011，a2011)，则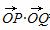等于(　　)

    A．2011  B．－2011  C．0  D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，点(an＋2，Sn＋1)在直线y＝4x－5上，其中n∈N*.令bn＝an＋1－2an，且a1＝1.

    (1)求数列{bn}的通项公式；

    (2)若f(x)＝b1x＋b2x2＋b3x3＋…＋bnxn，求f ′(1)的表达式．

    查看答案和解析>>

    同步练习册答案