
【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a﹣1)x+(a2﹣5)=0}
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
【答案】(1)a的值为-1或-3;
(2)a的取值范围是a≤-3.
【解析】
(1)根据条件A∩B={2},得到![]() ,代入方程,求得
,代入方程,求得![]() 的值,分类讨论即可求解;
的值,分类讨论即可求解;
(2)由A∪B=A,转化为![]() ,然后分类讨论,建立关系式,即可求解实数
,然后分类讨论,建立关系式,即可求解实数![]() 的取值范围.
的取值范围.
解:由x2-3x+2=0得x=1或x=2,
故集合A={1,2}.
(1)∵A∩B={2},∴2∈B,代入B中的方程,
得a2+4a+3=0a=-1或a=-3.
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件.
综上,a的值为-1或-3.
(2)对于集合B,
Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴BA.
①当Δ<0,即a<-3时,B=,满足条件;
②当Δ=0,即a=-3时,B={2},满足条件;
③当Δ>0,即a>-3时,B=A={1,2}才能满足条件,
则由根与系数的关系得![]()
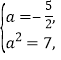 矛盾.
矛盾.
综上,a的取值范围是{a|a≤-3}.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知全集U={1,2,3,4,5,6,7},集合A={1,3,7},B={x|x=log2(a+1),a∈A},则A∩B=( )
A.{1,3}
B.{5,6}
C.{4,5,6}
D.{4,5,6,7}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率
的离心率 ![]() ,过点A(0,﹣b)和B(a,0)的直线与原点的距离为
,过点A(0,﹣b)和B(a,0)的直线与原点的距离为 ![]() .
.
(1)求椭圆的方程;
(2)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点,问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于圆锥曲线的命题中
①设![]() 是两个定点,
是两个定点, ![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线的一支;②过定圆
的轨迹为双曲线的一支;②过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
, ![]() 为坐标原点,若
为坐标原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;③方程
的轨迹为椭圆;③方程![]() 的两根可分别作为椭圆和双曲线的离心率;④双曲线
的两根可分别作为椭圆和双曲线的离心率;④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上任意一点,点
上任意一点,点![]() 与点
与点![]() 关于原点对称,线段
关于原点对称,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于
交于![]() 点.
点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() 使以
使以![]() 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30人,则每人收取培训费1000元;若参加培训的员工人数超过30人,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算:公司此次培训的总费用最多需要多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种大型商品,A,B两地都有出售,且价格相同,某地居民从两地之一购得商品后,运回的费用是:每单位距离A地的运费是B地运费的3倍.已知A,B两地相距10 km,顾客选A或B地购买这件商品的标准是:包括运费和价格的总费用较低.求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点![]() 是抛物线
是抛物线![]() 上一定点,直线
上一定点,直线![]() 的斜率互为相反数,且与抛物线另交于
的斜率互为相反数,且与抛物线另交于![]() 两个不同的点.
两个不同的点.

(1)求点![]() 到其准线的距离;(2)求证:直线
到其准线的距离;(2)求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com