
分析 (1)将题中特殊角的三角函数值代入原式,利用两角和的正切函数公式化简可得答案.
(2)将题中特殊角的三角函数值代入原式,利用两角差的正切函数公式化简可得答案.
(3)将题中特殊角的三角函数值代入原式,利用两角和的正切函数公式化简可得答案.
(4)利用两角和的正切函数公式化简可得答案.
解答 解:(1)$\frac{1+tan15°}{1-tan15°}$=$\frac{tan45°+tan15°}{1-tan45°tan15°}$=tan60°=$\sqrt{3}$;
(2)$\frac{\sqrt{3}-tan15°}{1+\sqrt{3}tan15°}$=$\frac{tan60°-tan15°}{1+tan60°tan15°}$=tan(60°-15°)=tan45°=1;
(3)tan21°+tan24°+tan21°tan24°=tan(21°+24°)(1-tan21°tan24°)+tan21°tan24°=1-tan21°tan24°+tan21°tan24°=1;
(4)tanα+tan($\frac{π}{3}$-α)+$\sqrt{3}$tanαtan($\frac{π}{3}$-α)=tan(α+$\frac{π}{3}$-α)(1-tanαtan($\frac{π}{3}$-α))+$\sqrt{3}$tanαtan($\frac{π}{3}$-α)=$\sqrt{3}$-$\sqrt{3}$tanαtan($\frac{π}{3}$-α)+$\sqrt{3}$tanαtan($\frac{π}{3}$-α)=$\sqrt{3}$.
点评 本题主要考查了特殊角的三角函数值,两角和的正切函数公式在三角函数化简求值中的应用,熟记特殊角的三角函数是解题的关键,属于基础题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年新疆库尔勒市高二上学期分班考试数学(理)试卷(解析版) 题型:填空题
已知两条不同直线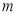 、
、 ,两个不同平面
,两个不同平面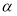 、
、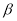 ,给出下列命题:
,给出下列命题:
①若 垂直于
垂直于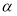 内的两条相交直线,则
内的两条相交直线,则 ⊥
⊥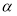 ;
;
②若 ∥
∥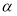 ,则
,则 平行于
平行于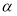 内的所有直线;
内的所有直线;
③若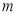
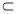
 ,
,
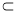
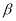 且
且 ⊥
⊥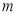 ,则
,则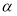 ⊥
⊥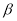 ;
;
④若
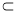
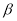 ,
,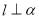 ,则
,则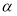 ⊥
⊥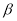 ;
;
⑤若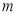
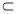
 ,
,
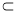
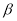 且
且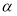 ∥
∥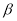 ,则
,则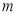 ∥
∥ ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com