Question

12．“$\frac{ln3-5}{3}$≤k≤$\frac{ln2-1}{2}$”是“关于x的不等式lnx+x+1＞x²+kx有且仅有2个正整数解”的（　　）

• A． 充分不必要条件
• B． 必要不充分条件
• C． 充要条件
• D． 既不充分也不必要条件

Answer 1

分析 由图可求得“关于x的不等式lnx+x+1＞x²+kx有且仅有2个正整数解”的k的取值范围，结合充要条件的定义，可得答案．

解答 解：关于x的不等式lnx+x+1＞x²+kx
即$\frac{lnx}{x}$$+1+\frac{1}{x}$-x＞k，
设y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x，
则y′=$\frac{{x}^{2}+lnx}{{x}^{2}}$，
令y′=-$\frac{{x}^{2}+lnx}{{x}^{2}}$的零点为a，则a∈（0，1），且
当x∈（0，a）时，y′＞0，y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x为增函数，
当x∈（a，+∞）时，y′＞0，y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x为减函数，
故函数y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x的图象如下图所示：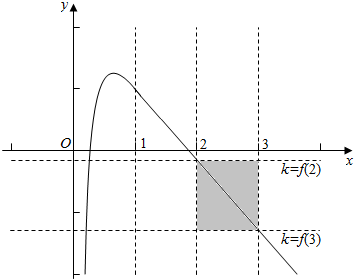

要使$\frac{lnx}{x}$$+1+\frac{1}{x}$-x＞k有且仅有2个正整数解，
则k∈[$\frac{ln3}{3}+1+\frac{1}{3}-3$，$\frac{ln2}{2}+1+\frac{1}{2}-2$），
即$\frac{ln3-5}{3}$≤k＜$\frac{ln2-1}{2}$”，
故“$\frac{ln3-5}{3}$≤k≤$\frac{ln2-1}{2}$”是“关于x的不等式lnx+x+1＞x²+kx有且仅有2个正整数解”的必要不充分条件，
故选：B．

点评 本题考查的知识点是充要条件的定义，存在性问题，数形结合思想，其中求出“关于x的不等式lnx+x+1＞x²+kx有且仅有2个正整数解”的充要条件，难度较大．