解:(1)求导函数,可得f′(x)=3x
2+2a x+b.
由题设,∵函数f(x)=x
3+ax
2+bx+c在x=1与
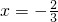
时,都取得极值.
∴x=1,x=-

为f′(x)=0的解.
∴-

a=1-

,

=1×(-

).
解得a=-

,b=-2(4分)
此时,f′(x)=3x
2-x-2=(x-1)(x+

),x=1与
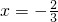
都是极值点.(5分)
(2)f (x)=x
3-

x
2-2 x+c,由f (-1)=-1-

+2+c=

,∴c=1.
∴f (x)=x
3-

x
2-2 x+1.
| x | (-∞,- ) ) | (- ,1) ,1) | (1,+∞) |
| f′(x) | + | - | + |
∴f (x)的递增区间为(-∞,-

),及(1,+∞),递减区间为(-

,1).
当x=-

时,f (x)有极大值,f (-

)=
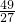
;
当x=1时,f (x)有极小值,f (1)=-

(10分)
(3)由(1)得,f′(x)=(x-1)(3x+2),f (x)=x
3-

x
2-2 x+c,
f (x)在[-1,-

)及(1,2]上递增,在(-

,1)递减.
而f (-

)=-

-

+

+c=c+
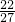
,f (2)=8-2-4+c=c+2.
∴f (x)在[-1,2]上的最大值为c+2.
∴

∴

∴

或

∴0<c<1或c<-3(16分)
分析:(1)求出f′(x)并令其等于0得到方程,把x=1,x=-

代入求出a、b即可;
(2)利用函数与导函数,建立表格,根据导数的正负,确定函数的单调性,从而确定函数的极值;
(3)求出函数的最大值为f(2),要使对x∈[-1,2]都有
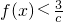
恒成立,利用函数的最大值,建立不等式,从而可求出c的取值范围.
点评:本题考查利用导数求函数极值,利用导数研究函数单调性,以及恒成立问题的处理,解题的关键是正确求出导函数.

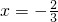 时,都取得极值.
时,都取得极值.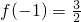 ,求f(x)的单调区间和极值;
,求f(x)的单调区间和极值;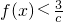 恒成立,求c的取值范围.
恒成立,求c的取值范围.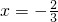 时,都取得极值.
时,都取得极值. 为f′(x)=0的解.
为f′(x)=0的解. a=1-
a=1- ,
, =1×(-
=1×(- ).
). ,b=-2(4分)
,b=-2(4分) ),x=1与
),x=1与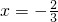 都是极值点.(5分)
都是极值点.(5分) x2-2 x+c,由f (-1)=-1-
x2-2 x+c,由f (-1)=-1- +2+c=
+2+c= ,∴c=1.
,∴c=1. x2-2 x+1.
x2-2 x+1. )
) ,1)
,1) ),及(1,+∞),递减区间为(-
),及(1,+∞),递减区间为(- ,1).
,1). 时,f (x)有极大值,f (-
时,f (x)有极大值,f (- )=
)=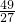 ;
; (10分)
(10分) x2-2 x+c,
x2-2 x+c, )及(1,2]上递增,在(-
)及(1,2]上递增,在(- ,1)递减.
,1)递减. )=-
)=- -
- +
+ +c=c+
+c=c+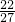 ,f (2)=8-2-4+c=c+2.
,f (2)=8-2-4+c=c+2.

 或
或
 代入求出a、b即可;
代入求出a、b即可;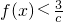 恒成立,利用函数的最大值,建立不等式,从而可求出c的取值范围.
恒成立,利用函数的最大值,建立不等式,从而可求出c的取值范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<