
(12分)一个圆锥,它的底面直径和高均为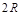 .
.
(1)求这个圆锥的表面积和体积.
(2)在该圆锥内作一内接圆柱,当圆柱的底面半径和高分别为多少时,它的侧面积最大?最大值是多少?
(1)  。
。
(2)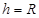 时,圆柱的侧面积
时,圆柱的侧面积 取得最大值,其最大值为
取得最大值,其最大值为 。
。
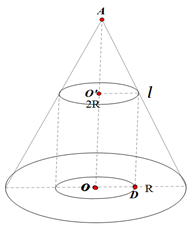
解析试题分析:(1) 如图,设母线长为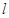 ,
,
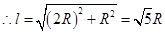 ....................1分
....................1分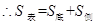 ...................................2分
...................................2分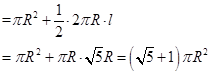 ...........................3分
...........................3分 .....................5分
.....................5分
(2)设圆柱的高为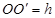 ,底面半径为
,底面半径为
 ,侧面积为
,侧面积为
则 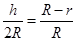 ..............................7分
..............................7分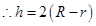 .........................8分
.........................8分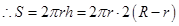 ..............9分
..............9分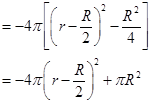 ................10分
................10分
当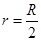 时,即
时,即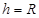 时,圆柱的侧面积
时,圆柱的侧面积 取得最大值,其最大值为
取得最大值,其最大值为 ....12分
....12分
考点:本题主要考查圆柱、圆锥的几何特征,体积计算及面积计算,二次函数的图象和性质。
点评:综合题,组合体问题中要注意观察几何元素之间的关系,并注意将“空间问题”转化成“平面问题”,这里运用了相似三角形相关知识。本题较难。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
正四棱柱ABCD-A1B1C1D1的底面边长是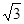 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.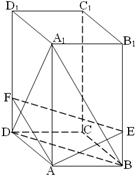
(1)求证:A1C⊥面AEF;
(2)求截面AEF与底面ABCD所成二面角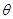 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某建筑物的上半部分是多面体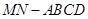 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.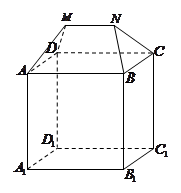

(Ⅰ)求直线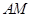 与平面
与平面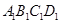 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角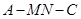 的余弦值;
的余弦值;
(Ⅲ)求该建筑物的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题9分)如图是一个空间几何体的三视图,其正视图与侧视图是边长为4cm的正三角形、俯视图中正方形的边长为4cm,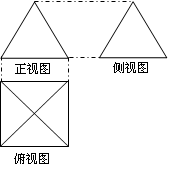
(1)画出这个几何体的直观图(不用写作图步骤);
(2)请写出这个几何体的名称,并指出它的高是多少;
(3)求出这个几何体的表面积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA1平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:AE⊥PD‘
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为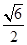 求二面角E-AF-C的余弦值
求二面角E-AF-C的余弦值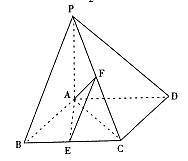
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com