
【题目】在奥运知识有奖问答竞赛中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲答对这道题的概率是![]() ,甲、乙两人都回答错误的概率是
,甲、乙两人都回答错误的概率是![]() ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是![]() .设每人回答问题正确与否相互独立的.
.设每人回答问题正确与否相互独立的.
(Ⅰ)求乙答对这道题的概率;
(Ⅱ)求甲、乙、丙三人中,至少有一人答对这道题的概率.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)设乙答对这道题的概率为![]() ,由对立事件概率关系和相互独立事件概率乘法公式,求出乙答对这道题的概率;
,由对立事件概率关系和相互独立事件概率乘法公式,求出乙答对这道题的概率;
(Ⅱ)设丙答对这道题的概率![]() ,由相互独立事件概率乘法公式,求出丙答对这道题的概率和甲、乙、丙三人都回答错误的概率,再由对立事件的概率公式,求得答案.
,由相互独立事件概率乘法公式,求出丙答对这道题的概率和甲、乙、丙三人都回答错误的概率,再由对立事件的概率公式,求得答案.
详解:解:(Ⅰ)记甲、乙、丙3人独自答对这道题分别为事件![]() ,
,
设乙答对这道题的概率![]() ,
,
由于每人回答问题正确与否是相互独立的,因此![]() 是相互独立事件.
是相互独立事件.
由题意,并根据相互独立事件同时发生的概率公式,
得![]()
解得![]() ,
,
所以,乙对这道题的概率为![]()
(Ⅱ)设“甲、乙、丙、三人中,至少有一人答对这道题”为事件![]() ,丙答对这道题的概率
,丙答对这道题的概率![]() .
.
由(Ⅰ),并根据相互独立事件同时发生的概率公式,
得![]() ,
,
解得![]()
甲、乙、丙三人都回答错误的概率为![]()
![]()
![]()
因为事件“甲、乙、丙三人都回答错误”与事件“甲、乙、丙三人中,至少有一人答对这道题”是对立事件,
所以,所求事件概率为![]()


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围;
(2)当b=1时,若对任意x∈[0,1],-1≤f(x)≤1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(坐标系与参数方程选做题)
已知曲线C的参数方程为 ![]() (t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
(t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
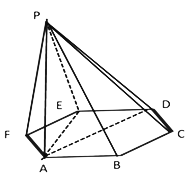
【题目】如图,已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面
平面![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①![]() ;
;
②直线![]() 平面
平面![]() ;
;
③平面![]() 平面
平面![]() ;
;
④异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
其中正确的有_______(把所有正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1 , A2 , …,A9和B1 , B2 , …,B9 , 连接OBi , 过Ai作x轴的垂线与OBi , 交于点 ![]() .
. 
(1)求证:点 ![]() 都在同一条抛物线上,并求抛物线E的方程;
都在同一条抛物线上,并求抛物线E的方程;
(2)过点C作直线l与抛物线E交于不同的两点M,N,若△OCM与△OCN的面积之比为4:1,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com