【题目】如图，四边形
是平行四边形，平面
平面，
，
，
，
，
，
，
为
的中点．
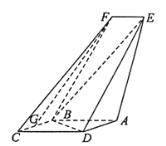
（1）求证：
平面
；
（2）求证：平面
平面
.
科目：高中数学 来源： 题型：
【题目】已知某中学高三学生共有800人参加了数学与英语水平测试，现学校决定利用随机数表法从中抽取100人的成绩进行统计，先将800人按001，002，…，800进行编号．
如果从第8行第7列的数开始从左向右读，（下面是随机数表的第7行至第9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 26
83 92 53 16 59 16 92 75 35 62 98 21 50 71 75 12 86 73 63 01
58 07 44 39 13 26 33 21 13 42 78 64 16 07 82 52 07 44 38 15
则最先抽取的2个人的编号依次为_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，已知点A（5，－2），B（7,3），且边AC的中点M在y轴上，边BC的中点N在x轴上，求：
（1）顶点C的坐标；
（2）直线MN的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中,已知直线
的参数方程为
(
为参数),以坐标原点为极点,以
轴正半轴为极轴建立极坐标系,曲线
的极坐标方程为
，直线与曲线交于
两点.
(1)求直线l的普通方程和曲线的直角坐标方程;
(2)已知点
的极坐标为
,求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数1，3，6，10，…，第n个三角形数为 
．记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：
三角形数 
，
正方形数N（n，4）=n2 ，
五边形数 
，
六边形数N（n，6）=2n2﹣n，
…
可以推测N（n，k）的表达式，由此计算N（10，24）= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
：
，点
是直线
：
上的一动点，过点作圆M的切线
、
，切点为
、
．
（Ⅰ）当切线PA的长度为
时，求点的坐标；
（Ⅱ）若
的外接圆为圆
，试问：当运动时，圆是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由；
（Ⅲ）求线段
长度的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在奥运知识有奖问答竞赛中，甲、乙、丙三人同时回答一道有关奥运知识的问题，已知甲答对这道题的概率是
，甲、乙两人都回答错误的概率是
，乙、丙两人都回答正确的概率是
.设每人回答问题正确与否相互独立的.
(Ⅰ）求乙答对这道题的概率；
（Ⅱ）求甲、乙、丙三人中，至少有一人答对这道题的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
