
【题目】已知圆![]() :
:![]() ,点
,点![]() 是直线
是直线![]() :
:![]() 上的一动点,过点
上的一动点,过点![]() 作圆M的切线
作圆M的切线![]() 、
、![]() ,切点为
,切点为![]() 、
、![]() .
.
(Ⅰ)当切线PA的长度为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(Ⅱ)若![]() 的外接圆为圆
的外接圆为圆![]() ,试问:当
,试问:当![]() 运动时,圆
运动时,圆![]() 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(Ⅲ)求线段![]() 长度的最小值.
长度的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)AB有最小值
;(Ⅲ)AB有最小值![]()
【解析】
试题(Ⅰ)求点的坐标,需列出两个独立条件,根据解方程组解:由点![]()
![]() 是直线
是直线![]() :
:![]() 上的一动点,得
上的一动点,得![]() ,由切线PA的长度为
,由切线PA的长度为![]() 得
得![]() ,解得
,解得![]() (Ⅱ)设P(2b,b),先确定圆
(Ⅱ)设P(2b,b),先确定圆![]() 的方程:因为∠MAP=90°,所以经过A、P、M三点的圆
的方程:因为∠MAP=90°,所以经过A、P、M三点的圆![]() 以MP为直径,其方程为:
以MP为直径,其方程为: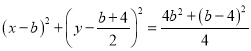 ,再按b整理:
,再按b整理:![]() 由
由![]() 解得
解得![]() 或
或![]() ,所以圆过定点
,所以圆过定点![]() (Ⅲ)先确定直线
(Ⅲ)先确定直线![]() 方程,这可利用两圆公共弦性质解得:由圆
方程,这可利用两圆公共弦性质解得:由圆![]() 方程为
方程为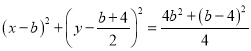 及 圆
及 圆![]() :
:![]() ,相减消去x,y平方项得圆
,相减消去x,y平方项得圆![]() 方程与圆
方程与圆![]() 相交弦AB所在直线方程为:
相交弦AB所在直线方程为:![]() ,相交弦长即:
,相交弦长即:
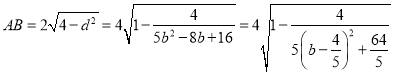 ,当
,当![]() 时,AB有最小值
时,AB有最小值![]()
试题解析:(Ⅰ)由题可知,圆M的半径r=2,设P(2b,b),
因为PA是圆M的一条切线,所以∠MAP=90°,
所以MP=![]() ,解得
,解得![]()
所以![]() 4分
4分
(Ⅱ)设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆![]() 以MP为直径,
以MP为直径,
其方程为: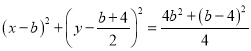
即![]()
由![]() , 7分
, 7分
解得![]() 或
或![]() ,所以圆过定点
,所以圆过定点![]() 9分
9分
(Ⅲ)因为圆![]() 方程为
方程为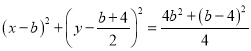
即![]() ①
①
圆![]() :
:![]() ,即
,即![]() ②
②
②-①得圆![]() 方程与圆
方程与圆![]() 相交弦AB所在直线方程为:
相交弦AB所在直线方程为:
![]() 11分
11分
点M到直线AB的距离![]() 13分
13分
相交弦长即:
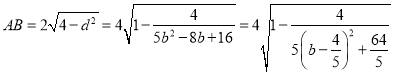
当![]() 时,AB有最小值
时,AB有最小值![]() 16分
16分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了更好地服务民众,某共享单车公司通过![]() 向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用
向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
(I)求用户骑行一次获得0元奖券的概率;
(II)若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围;
(2)当b=1时,若对任意x∈[0,1],-1≤f(x)≤1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面
平面![]() ,
,![]() ,给出下列结论:
,给出下列结论:
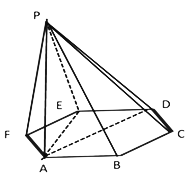
①![]() ;
;
②直线![]() 平面
平面![]() ;
;
③平面![]() 平面
平面![]() ;
;
④异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
其中正确的有_______(把所有正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com