Question

1．已知△ABC中，∠C=90°，AC=BC，则下列等式成立的是①②③④（填序号）
①|$\overrightarrow{CA}$-$\overrightarrow{CB}$|=|$\overrightarrow{CA}$+$\overrightarrow{CB}$|②|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=|$\overrightarrow{BA}$-$\overrightarrow{BC}$|
③|$\overrightarrow{CA}$-$\overrightarrow{BA}$|=|$\overrightarrow{CB}$-$\overrightarrow{AB}$|④|$\overrightarrow{CA}$+$\overrightarrow{CB}$|²=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|²+|$\overrightarrow{BA}$-$\overrightarrow{CA}$|²．

Answer 1

分析 根据条件作出正方形ACBD，根据向量的线性运算法则和正方形的性质判断．

解答 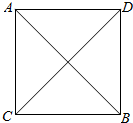解：以AC，BC为邻边作平行四边形ACBD，∵∠ACB=90°，AC=BC，∴四边形ACBD是正方形．
∵|$\overrightarrow{CA}$-$\overrightarrow{CB}$|=|$\overrightarrow{BA}$|=AB，|$\overrightarrow{CA}$+$\overrightarrow{CB}$|=|$\overrightarrow{CD}$|=CD，∴①正确；
②|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=|$\overrightarrow{CB}$|=BC，|$\overrightarrow{BA}$-$\overrightarrow{BC}$|=|$\overrightarrow{CA}$|=AC，∴②正确；
③|$\overrightarrow{CA}$-$\overrightarrow{BA}$|=|$\overrightarrow{CB}$|=BC，|$\overrightarrow{CB}$-$\overrightarrow{AB}$|=|$\overrightarrow{CA}$|=AC，∴③正确；
④|$\overrightarrow{CA}$+$\overrightarrow{CB}$|²=|$\overrightarrow{CD}$|²=CD²，|$\overrightarrow{AB}$-$\overrightarrow{AC}$|²=|$\overrightarrow{CB}$|²=CB²，|$\overrightarrow{BA}$-$\overrightarrow{CA}$|²=|$\overrightarrow{BC}$|²=BC²=BD²，∴④正确．
故答案为①②③④．

点评 本题考查了平面向量线性运算的几何意义，属于基础题．