
分析 (1)根据函数的图象经过点(0,1),求得φ的值,再根据周期性求得ω,可得函数f(x)的解析式.
(2)由条件求得sinα+cosα=$\frac{2}{3}$,平方可得sinαcosα的值,从而求得sinα-cosα 的值,再利用诱导公式化简要求的式子,可得结果.
解答 解:(1)根据函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)的图象经过点(0,1),
可得sinφ=1,∴φ=$\frac{π}{2}$,.
∵其相邻两对称轴之间的距离为π,∴$\frac{1}{2}$•$\frac{2π}{ω}$=π,求得ω=1,∴f(x)=sin(x+$\frac{π}{2}$)=cosx.
(2)∵sinα+f(α)=$\frac{2}{3}$,α∈(0,π),即 sinα+cosα=$\frac{2}{3}$,平方可得sinαcosα═-$\frac{5}{18}$,
∴α为钝角,sinα-cosα=$\sqrt{{(sinα-cosα)}^{2}}$=$\frac{\sqrt{14}}{3}$,
∴$\frac{sin(-α)sin(π+α)+sinαcos(π-α)}{1+tan(3π+α)}$=$\frac{-sinα•(-sinα)+sinα•(-cosα)}{1+tanα}$=$\frac{sinαcosα•(sinα-cosα)}{cosα+sinα}$
=$\frac{-\frac{5}{18}•\frac{\sqrt{14}}{3}}{\frac{2}{3}}$=-$\frac{5}{36}$$\sqrt{14}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,三角函数的化简求值,属于基础题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:解答题
如图,在四棱锥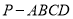 中,底面
中,底面 是直角梯形,
是直角梯形,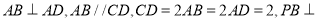 底面
底面 ,
,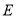 是
是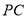 上的点.
上的点.

(1)求证: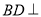 平面
平面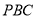 ;
;
(2)设 ,若
,若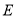 是
是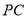 的中点,且直线
的中点,且直线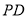 与平面
与平面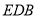 所成角的正弦值为
所成角的正弦值为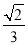 ,求二面角
,求二面角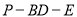 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2017届湖南石门县一中高三9月月考数学(文)试卷(解析版) 题型:解答题
已知函数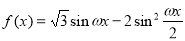 (
(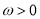 )的最小正周期为
)的最小正周期为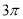 .
.
(1)求函数 在区间
在区间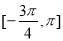 上的最大值和最小值;
上的最大值和最小值;
(2)已知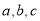 分别为锐角三角形
分别为锐角三角形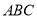 中角
中角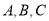 的对边,且满足
的对边,且满足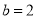 ,
,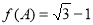 ,
,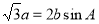 ,求
,求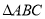 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(|x|)=x | B. | f(|x|)=x2+2x | C. | f(|x+1|)=x | D. | f(|x+1|)=x2+2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com