
 已知点P是双曲线$\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{64}$=1的右支上一点,F1、F2分别为双曲线的左、右焦点,I为△PF1F2的内心,若${S}_{△I{PF}_{1}}$=${S}_{△I{PF}_{2}}$+λ${S}_{△{{IF}_{1}F}_{2}}$成立,则λ的值为( )
已知点P是双曲线$\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{64}$=1的右支上一点,F1、F2分别为双曲线的左、右焦点,I为△PF1F2的内心,若${S}_{△I{PF}_{1}}$=${S}_{△I{PF}_{2}}$+λ${S}_{△{{IF}_{1}F}_{2}}$成立,则λ的值为( )| A. | $\frac{5}{8}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
分析 先由${S}_{△I{PF}_{1}}$=${S}_{△I{PF}_{2}}$+λ${S}_{△{{IF}_{1}F}_{2}}$得|PF1=|PF2|+λ|F1F2|=|PF2|+λ•2c,再由P是右支上的点,得到|PF1|=|PF2|+2a,由此能够求出λ的值.
解答 解:依题意,设△PF1F2的内切圆的半径为r,
则${S}_{△I{PF}_{1}}$=$\frac{1}{2}$|PF1|•r,${S}_{△I{PF}_{2}}$=$\frac{1}{2}$|PF2|,${S}_{△{{IF}_{1}F}_{2}}$=$\frac{1}{2}$|F1F2|•r,
∵${S}_{△I{PF}_{1}}$=${S}_{△I{PF}_{2}}$+λ${S}_{△{{IF}_{1}F}_{2}}$
∴|PF1|-|PF2|=-λ|F1F2|,
∵P为双曲线右支上一点,
∴2a=λ×2c,由双曲线的方程可知,a=6,b=8,故c=10,
∴λ=$\frac{2a}{2c}$=$\frac{3}{5}$.
故选C.
点评 本题考查抛物线的定义,三角形的面积公式,考查双曲线的性质和应用,解题时要认真审题,注意公式的灵活运用,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
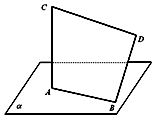 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.9544 | C. | 0.2718 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com