
 ,
,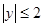 ,点
,点 的坐标为
的坐标为
 时,求
时,求 的坐标满足
的坐标满足 的概率。
的概率。 时,求
时,求 的坐标满足
的坐标满足 的概率。
的概率。 的坐标满足
的坐标满足 的概率是
的概率是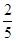 ;
; 的坐标满足
的坐标满足 的概率是
的概率是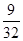 。
。 的坐标满足
的坐标满足 ”为事件
”为事件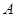 ,事件
,事件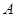 包含的基本事件有10种,所有的情况有当
包含的基本事件有10种,所有的情况有当 时,这是一个古典概型
时,这是一个古典概型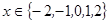 ,
,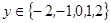
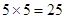 种,利用古典概型得到结论。
种,利用古典概型得到结论。 的坐标满足
的坐标满足 ”为事件
”为事件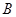
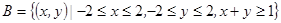 ,那么利用面积比得到结论。
,那么利用面积比得到结论。 得
得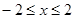 ,由
,由 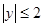 得
得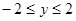 ,
,  时,这是一个古典概型
时,这是一个古典概型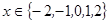 ,
,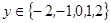 ………1分
………1分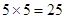 种。…………………………2分
种。…………………………2分 的坐标满足
的坐标满足 ”为事件
”为事件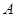 ……………………3分
……………………3分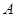 包含的基本事件有
包含的基本事件有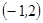 ,
,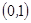 ,
,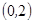 ,
,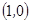 ,
,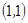 ,
,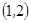 ,
,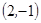
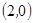 ,
,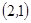 ,
,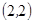 共10种。……………………………5分
共10种。……………………………5分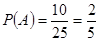 …………………………………6分
…………………………………6分 的坐标满足
的坐标满足 的概率是
的概率是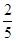 ………………………………7分
………………………………7分 时,这是一个几何概型
时,这是一个几何概型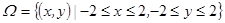 …………………8分
…………………8分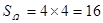 ……………………………9分
……………………………9分 的坐标满足
的坐标满足 ”为事件
”为事件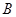 ……………………10分
……………………10分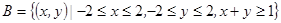 即下图阴影部分
即下图阴影部分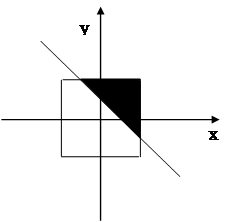
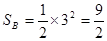 …………………………12分
…………………………12分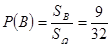 ………………………13分
………………………13分 的坐标满足
的坐标满足 的概率是
的概率是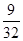 ………14分
………14分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 ,集合
,集合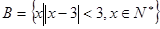 ,
,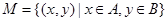
 所有可能的结果;
所有可能的结果;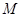 中任取一个元素,求“
中任取一个元素,求“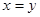 ”的概率
”的概率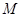 中任取一个元素,求“
中任取一个元素,求“ ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况 |
B.一枚硬币掷一次得到正面的概率是 ,那么掷两次一定会出现一次正面的情况 ,那么掷两次一定会出现一次正面的情况 |
| C.如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元 |
| D.随机事件发生的概率与试验次数无关 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 视觉 视觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | 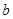 | |
| 偏高 | 2 | 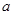 | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
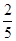 .
.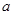 、
、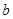 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的样本,已知每位学生被抽到的概率都为
的样本,已知每位学生被抽到的概率都为 ,则
,则 ▲ .
▲ .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com