
(本小题满分12分)已知函数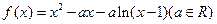 .
.
(1) 当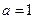 时,求函数
时,求函数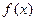 的最值;
的最值;
(2) 求函数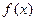 的单调区间;
的单调区间;
(3)(仅385班、389班学生做) 试说明是否存在实数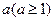 使
使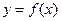 的图象与
的图象与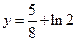 无公共点.
无公共点.
科目:高中数学 来源: 题型:解答题
(本题14分)已知函数f (x) = ax3 +x2 -ax,其中a,x∈R.
(Ⅰ)若函数f (x)在区间(1,2)上不是单调函数,试求a的取值范围;
(Ⅱ)直接写出(不需给出运算过程)函数 的单调递减区间;
的单调递减区间;
(Ⅲ)如果存在a∈(-∞,-1],使得函数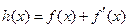 , x∈[-1, b](b > -1),在x = -1处取得最小值,试求b的最大值.
, x∈[-1, b](b > -1),在x = -1处取得最小值,试求b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知二次函数
为常数) ;
; .若直线
.若直线 1、
1、 2与函数
2与函数 的图象以及
的图象以及 2,y轴与函数
2,y轴与函数 的图象
的图象
所围成的封闭图形如阴影所示.
(1)求
 、b、c的值;
、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若 问是否存在实数m,使得
问是否存在实数m,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位: 资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果 的费用为y(元)(不计返程费用),将y表示成速度v的函数
的费用为y(元)(不计返程费用),将y表示成速度v的函数 关系式;
关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com