
分析 (Ⅰ)求出原函数的导函数,然后分a≥0和-1<a<0讨论,利用导函数大于0和小于0分别求出x的取值范围求得f(x)的单调区间;
(Ⅱ)假设存在两点A(x1、y1)、B(x2,y2),不妨设0<x1<x2,利用两点求斜率公式求出过A,B的直线的斜率,把A,B中点的横坐标用A,B的坐标表示,求导得到曲线在A,B中点处的切线的斜率,列等式后化简,令$\frac{x_2}{x_1}=t$,则t>1,则$lnt=\frac{2(t-1)}{t+1}$,令$g(t)=lnt-\frac{2(t-1)}{t+1}(t>1)$,利用导数说明该函数无零点,说明在函数y=f(x)的图象上不存在两点A、B,使得直线AB存在中值伴随切线.
解答 解:(Ⅰ)$f'(x)=\frac{1}{x}-ax+a-1$=$\frac{{-a{x^2}+(a-1)x+1}}{x}=-\frac{(ax+1)(x-1)}{x}(x>0)$,
①当a≥0时,$\frac{-(ax+1)}{x}<0$,
由$\left\{\begin{array}{l}f'(x)>0\\ x>0\end{array}\right.⇒0<x<1$,
由$\left\{\begin{array}{l}f'(x)<0\\ x>0\end{array}\right.⇒x>1$,
∴f(x)的增区间为(0,1),减区间为(1,+∞);
②当-1<a<0时,则$-\frac{1}{a}>1$,
由$\left\{\begin{array}{l}f'(x)>0\\ x>0\end{array}\right.⇒0<x<1$或$x>-\frac{1}{a}$,
由$\left\{\begin{array}{l}f'(x)<0\\ x>0\end{array}\right.⇒1<x<-\frac{1}{a}$,
∴f(x)的增区间为(0,1),$(-\frac{1}{a},+∞)$,减区间为$(1,-\frac{1}{a})$;
(Ⅱ)在函数y=f(x)的图象上不存在两点A、B,使得直线AB存在中值伴随切线.
证明如下:
假设存在两点A(x1、y1)、B(x2,y2),不妨设0<x1<x2,
则${y_1}=ln{x_1}-\frac{1}{2}a{x_1}^2+(a-1){x_1}$,${y_2}=ln{x_2}-\frac{1}{2}a{x_2}^2+(a-1){x_2}$,
∵${k_{AB}}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{(ln{x_2}-ln{x_1})-\frac{1}{2}a({x_2}^2-{x_1}^2)+(a-1)({x_2}-{x_1})}}{{{x_2}-{x_1}}}$
=$\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}-\frac{1}{2}a({x_2}+{x_1})+(a-1)$,
函数图象在${x_0}=\frac{{{x_1}+{x_2}}}{2}$处的切线的斜率$k=f'({x_0})=f'(\frac{{{x_1}+{x_2}}}{2})$=$\frac{2}{{{x_1}+{x_2}}}-\frac{a}{2}({x_1}+{x_2})+(a-1)$,
由$\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}-\frac{1}{2}a({x_2}+{x_1})+(a-1)=\frac{2}{{{x_2}+{x_1}}}-\frac{1}{2}a({x_2}+{x_1})+(a-1)$,
化简得:$\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}=\frac{2}{{{x_1}+{x_2}}}$,即$ln\frac{x_2}{x_1}=\frac{{2({x_2}-{x_1})}}{{{x_2}+{x_1}}}=\frac{{2(\frac{x_2}{x_1}-1)}}{{\frac{x_2}{x_1}+1}}$,
令$\frac{x_2}{x_1}=t$,则t>1,则$lnt=\frac{2(t-1)}{t+1}$,
令$g(t)=lnt-\frac{2(t-1)}{t+1}(t>1)$,则$g'(t)=\frac{1}{t}-\frac{4}{{{{(t+1)}^2}}}=\frac{{{{(t-1)}^2}}}{t(t+1)}$,
由t>1,得g′(t)>0,
∴g(t)在(1,+∞)上单调递增,
又g(t)在t=1处连续,g(t)>g(1)=0,
∴方程$lnt=\frac{2(t-1)}{t+1}$在t>1上无解,
因此在函数y=f(x)的图象上不存在A、B两点,使得直线AB存在中值伴随切线.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,体现了化归与转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
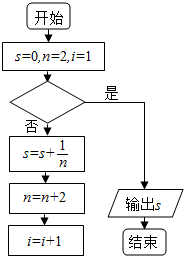
| A. | i>2016 | B. | i<2016 | C. | i>1008 | D. | i<1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4或5 | B. | 3或4 | C. | 3或2 | D. | 1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com