
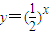 的图象上,且数列{an} 是a1=1,公差为d的等差数列.
的图象上,且数列{an} 是a1=1,公差为d的等差数列.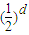 的等比数列;
的等比数列;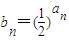 ,(1分)
,(1分)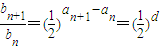 (常数),(4分)
(常数),(4分)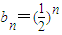 ,
,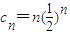 ,(7分)
,(7分)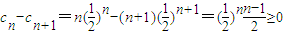 ,
,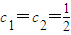 ,则
,则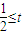 .最小的实数t等于
.最小的实数t等于 (12分)
(12分)

科目:高中数学 来源: 题型:
| OPn |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OPn |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(3×1006,-4[1-(![]() )1006]) B.(3×1004,-8[1-(
)1006]) B.(3×1004,-8[1-(![]() )1004])
)1004])
C.(3×1002,-4[1-(![]() )1002]) D.(3×1004,-4[1-(
)1002]) D.(3×1004,-4[1-(![]() )1004])
)1004])
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(3×1006,-4[1-(![]() )1006]) B.(3×1004,-8[1-(
)1006]) B.(3×1004,-8[1-(![]() )1004])
)1004])
C.(3×1 002,-4[1-(![]() )1002]) D.(3×1004,-4[1-(
)1002]) D.(3×1004,-4[1-(![]() )1004])
)1004])
查看答案和解析>>
科目:高中数学 来源:2007年广东省深圳市高考数学一模试卷(文科)(解析版) 题型:解答题
 ,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com