Question

8£®ÒÑÖªOΪԭµã£¬ÍÖÔ²C£º$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾b£¾0£©µÄ×󶥵ãΪE£¬É϶¥µãΪF£¬¹ýÍÖÔ²CµÄÓÒ½¹µã×÷xÖáµÄ´¹Ïß½»Ö±ÏßEFÓÚµãD£¬ÈôÖ±ÏßODбÂÊÊÇÖ±ÏßEFµÄбÂʵÄ$\sqrt{2}$+1±¶£®
£¨1£©ÇóÍÖÔ²CµÄÀëÐÄÂÊ£»
£¨2£©ÈôÍÖÔ²CµÄ½¹¾àΪ2$\sqrt{2}$£¬ÉèM£¨x₀£¬y₀£©ÎªÍÖÔ²CÉϵĶ¯µã£¬A£¨-2$\sqrt{2}$£¬0£©£¬Ö±ÏßAMÓëÍÖÔ²½»ÓÚÁíÒ»µãP£¬ÇÒ$\overrightarrow{AM}$=¦Ë$\overrightarrow{AP}$£¬ÊÔ̽ÌÖÊÇ·ñ´æÔÚʵÊým£¬Ê¹µÃmx₀-¦ËΪ¶¨Öµ£¿Èô´æÔÚ£¬Çó³ömµÄÖµ¼°´Ë¶¨Öµ£¬Èô²»´æÔÚ£¬Çë˵Ã÷ÀíÓÉ£®

Answer 1

·ÖÎö £¨1£©Ð´³öEFËùÔÚÖ±Ïß·½³Ì£¬µÃµ½DµÄ×ø±ê£¬ÓÉбÂʹØϵ¼´¿ÉÇóµÃÍÖÔ²ÀëÐÄÂÊ£»
£¨2£©ÓÉ£¨1£©ÖÐËùÇóÍÖÔ²ÀëÐÄÂʼ°½¹¾àÇóµÃa£¬ÔÙÓÉÒþº¬Ìõ¼þÇóµÃb£¬ÔòÍÖÔ²·½³Ì¿ÉÇó£¬Éè³öPµÃ×ø±ê£¬ÓÉÏòÁ¿µÈʽ°ÑMµÄ×ø±êÓÃPµÃ×ø±ê±íʾ£¬ÔÙÓÉMÔÚÍÖÔ²ÉϿɵõÈʽ$\sqrt{2}{x}_{0}-¦Ë=-3$£¬¼´´æÔÚʵÊým=$\sqrt{2}$£¬Ê¹µÃmx₀-¦ËΪ¶¨Öµ-3£®

½â´ð ½â£º£¨1£©Ö±ÏßEFµÄ·½³ÌΪy=$\frac{b}{a}£¨x+a£©$£¬½«x=c´úÈëµÃµãD£¨c£¬b+$\frac{bc}{a}$£©£¬
ÔòÖ±ÏßODµÄбÂÊΪ$\frac{b+\frac{bc}{a}}{c}=£¨\sqrt{2}+1£©¡Á\frac{b}{a}$£¬¿ÉµÃa=$\sqrt{2}c$£¬Ôòe=$\frac{c}{a}=\frac{\sqrt{2}}{2}$£»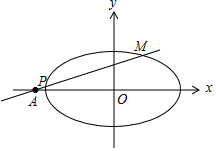
£¨2£©ÓÉ£¨1£©Öª$\frac{c}{a}=\frac{\sqrt{2}}{2}$£¬ÓÖ2c=2$\sqrt{2}$£¬
¡àc=$\sqrt{2}$£¬a=2£¬Ôòb²=a²-c²=2£¬
¡àÍÖÔ²CµÄ·½³ÌΪ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$£®
ÉèP£¨x₁£¬y₁£©£¬Ôò$\overrightarrow{AM}=£¨{x}_{0}+2\sqrt{2}£¬{y}_{0}£©$£¬$\overrightarrow{AP}=£¨{x}_{1}+2\sqrt{2}£¬{y}_{1}£©$£¬
ÓÉ$\overrightarrow{AM}=¦Ë\overrightarrow{AP}$£¬µÃ$\left\{\begin{array}{l}{{x}_{0}+2\sqrt{2}=¦Ë£¨{x}_{1}+2\sqrt{2}£©}\\{{y}_{0}=¦Ë{y}_{1}}\end{array}\right.$£¬
´Ó¶ø$\left\{\begin{array}{l}{{x}_{0}=¦Ë{x}_{1}+2\sqrt{2}£¨¦Ë-1£©}\\{{y}_{0}=¦Ë{y}_{1}}\end{array}\right.$£¬
¡ß$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{2}=1$£¬¡à$\frac{[¦Ë{x}_{1}+2\sqrt{2}£¨¦Ë-1£©]^{2}}{4}+\frac{£¨¦Ë{y}_{1}£©^{2}}{2}=1$£¬
¼´${¦Ë}^{2}£¨{{x}_{1}}^{2}+2{{y}_{1}}^{2}£©+4\sqrt{2}¦Ë£¨¦Ë-1£©{x}_{1}+8£¨¦Ë-1£©^{2}-4=0$£®
¡ß$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}=1$£¬¡à${{x}_{1}}^{2}+2{{y}_{1}}^{2}=4$£¬´úÈëµÃ$4{¦Ë}^{2}+4\sqrt{2}¦Ë£¨¦Ë-1£©{x}_{1}+8£¨¦Ë-1£©^{2}-4=0$£®
¼´$4\sqrt{2}¦Ë£¨¦Ë-1£©{x}_{1}+4£¨¦Ë-1£©£¨3¦Ë-1£©=0$£®
ÓÉÌâÒâÖª£¬¦Ë¡Ù1£®
¹Ê${x}_{1}=-\frac{3¦Ë-1}{\sqrt{2}¦Ë}$£¬¡à${x}_{0}=\frac{1+¦Ë}{\sqrt{2}}-2\sqrt{2}$£¬¼´$\sqrt{2}{x}_{0}-¦Ë=-3$£®
¹Ê´æÔÚʵÊým=$\sqrt{2}$£¬Ê¹µÃmx₀-¦ËΪ¶¨Öµ-3£®

µãÆÀ ±¾Ì⿼²éÍÖÔ²µÄ¼òµ¥ÐÔÖÊ£¬¿¼²éÁËÖ±ÏßÓëÍÖԲλÖùØϵµÄÓ¦Óã¬ÌåÏÖÁËÕûÌåÔËËã˼Ïë·½·¨£¬ÊÇÖеµÌ⣮