
【题目】已知A、B、C是椭圆M: ![]() =1(a>b>0)上的三点,其中点A的坐标为
=1(a>b>0)上的三点,其中点A的坐标为 ![]() ,BC过椭圆M的中心,且
,BC过椭圆M的中心,且 ![]() .
.
(1)求椭圆M的方程;
(2)过点(0,t)的直线l(斜率存在时)与椭圆M交于两点P、Q,设D为椭圆M与y轴负半轴的交点,且 ![]() ,求实数t的取值范围.
,求实数t的取值范围.
【答案】
(1)解:
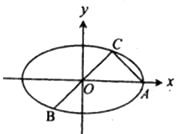
∵点A的坐标为 ![]() ,
,
∴ ![]() ,椭圆方程为
,椭圆方程为 ![]() ①
①
又∵ ![]() .,且BC过椭圆M的中心O(0,0),
.,且BC过椭圆M的中心O(0,0),
∴ ![]() .
.
又∵ ![]() ,
,
∴△AOC是以∠C为直角的等腰三角形,
易得C点坐标为( ![]() ,
, ![]() )
)
将( ![]() ,
, ![]() )代入①式得b2=4
)代入①式得b2=4
∴椭圆M的方程为 ![]()
(2)解:当直线l的斜率k=0,直线l的方程为y=t
则满足题意的t的取值范围为﹣2<t<2
当直线l的斜率k≠0时,设直线l的方程为y=kx+t
由 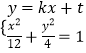
得(3k2+1)x2+6ktx+3t2﹣12=0
∵直线l与椭圆M交于两点P、Q,
∴△=(6kt)2﹣4(3k2+1)(3t2﹣12)>0
即t2<4+12k2 ②
设P(x1,y1),Q(x2,y2),x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
PQ中点H(x0,y0),
则H的横坐标 ![]() ,
,
纵坐标 ![]() ,
,
D点的坐标为(0,﹣2)
由 ![]() ,
,
得DH⊥PQ,kDHkPQ=﹣1,
即 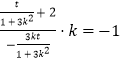 ,
,
即t=1+3k2. ③
∴k2>0,∴t>1.
由②③得0<t<4,
结合④得到1<t<4.
综上所述,﹣2<t<4.
【解析】(1)根据点A的坐标求出a,然后根据 ![]() 求出b,综合即可求出椭圆M的方程.(2)根据题意设出直线方程,与(1)中M的方程联立,然后运用设而不求韦达定理进行计算,求出实数t的取值范围.
求出b,综合即可求出椭圆M的方程.(2)根据题意设出直线方程,与(1)中M的方程联立,然后运用设而不求韦达定理进行计算,求出实数t的取值范围.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】为吸引顾客,某公司在商场举办电子游戏活动.对于![]() 两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏
两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏![]() ,若绿灯闪亮,获得
,若绿灯闪亮,获得![]() 分,若绿灯不闪亮,则扣除
分,若绿灯不闪亮,则扣除![]() 分(即获得
分(即获得![]() 分),绿灯闪亮的概率为
分),绿灯闪亮的概率为![]() ;玩一次游戏
;玩一次游戏![]() ,若出现音乐,获得
,若出现音乐,获得![]() 分,若没有出现音乐,则扣除
分,若没有出现音乐,则扣除![]() 分(即获得
分(即获得![]() 分),出现音乐的概率为
分),出现音乐的概率为![]() .玩多次游戏后累计积分达到
.玩多次游戏后累计积分达到![]() 分可以兑换奖品.
分可以兑换奖品.
(1)记![]() 为玩游戏
为玩游戏![]() 和
和![]() 各一次所得的总分,求随机变量
各一次所得的总分,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)记某人玩![]() 次游戏
次游戏![]() ,求该人能兑换奖品的概率.
,求该人能兑换奖品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x , x∈[﹣1,1],函数g(x)=[f(x)]2﹣2af(x)+3.
(1)当a=0时,求函数g(x)的值域;
(2)若函数g(x)的最小值为h(a),求h(a)的表达式;
(3)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2 , m2]?若存在,求出m,n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点P(4,﹣1)且与直线3x﹣4y+6=0垂直的直线方程是( )
A.4x+3y﹣13=0
B.4x﹣3y﹣19=0
C.3x﹣4y﹣16=0
D.3x+4y﹣8=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F为棱AD、AB的中点.
(Ⅰ)求证:EF∥平面CB1D1;
(Ⅱ)求证:平面CAA1C1⊥平面CB1D1 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+ax(x∈R).
(1)证明:当 a>2时,f(x)在 R上是增函数;
(2)若函数f(x)存在两个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,
, ![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com