
已知函数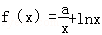 ,g(x)=
,g(x)=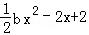 ,a,b∈R.
,a,b∈R.
(1)求函数f(x)的单调区间;
(2)记函数h(x)=f(x)+g(x),当a=0时,h(x)在(0,1)上有且只有一个极值点,求实数b的取值范围;
(3)记函数F(x)=|f(x)|,证明:存在一条过原点的直线l与y=F(x)的图象有两个切点.
(1)当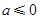 时,
时,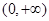 为单调增区间,
为单调增区间,
当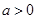 时,
时, 为单调减区间,
为单调减区间, 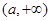 为单调增区间.
为单调增区间.
(2)b<1
(3)首先根据(1)的结论,讨论可得只有0<a< 时直线l与y=F(x)的图象有两个切点.设切点的横坐标分别为s、t且s<t,可得l与y=F(x)的图象有两个切点分别为直线l与曲线
时直线l与y=F(x)的图象有两个切点.设切点的横坐标分别为s、t且s<t,可得l与y=F(x)的图象有两个切点分别为直线l与曲线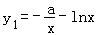 在x∈(s,t)的切点和曲线
在x∈(s,t)的切点和曲线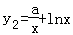 在x∈(t,+∞)的切点.由此结合直线的斜率公式和导数的几何意义列出关于a、x1、y1、x2、y2的关系式,化简整理可得
在x∈(t,+∞)的切点.由此结合直线的斜率公式和导数的几何意义列出关于a、x1、y1、x2、y2的关系式,化简整理可得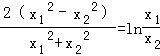 ,再令
,再令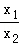 =k(0<k<1),转化为(k2+1)lnk=2k2﹣2.令G(k)=(k2+1)lnk﹣2k2+2,(0<k<1),由根的存在性定理证出:存在k0∈(0,1),使得G(k0)=0.由此即可得到原命题成立.
=k(0<k<1),转化为(k2+1)lnk=2k2﹣2.令G(k)=(k2+1)lnk﹣2k2+2,(0<k<1),由根的存在性定理证出:存在k0∈(0,1),使得G(k0)=0.由此即可得到原命题成立.
解析试题分析:(1)因为f'(x)=﹣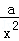 +
+ =
=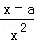 ,
,
①若a≤0,则f'(x)>0,f(x)在(0,+∞)上为增函数,…(2分)
②若a>0,令f'(x)=0,得x=a,
当0<x<a时,f'(x)<0;当x>a时,f'(x)>0.
所以(0,a)为单调减区间,(a,+∞)为单调增区间.
综上可得,当a≤0时,函数f(x)在(0,+∞)上为增函数,
当a>0时,函数f(x)的单调减区间为(0,a),单调增区间为(a,+∞). …(4分)
(2)a=0时,h(x)=f(x)+g(x)=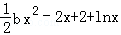 ,
,
∴h'(x)=bx﹣2+ =
=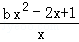 ,…(5分)
,…(5分)
h(x)在(0,1)上有且只有一个极值点,即h'(x)=0在(0,1)上有且只有一个根且不为重根,
由h'(x)=0得bx2﹣2x+1=0,…(6分)
( i)b=0,x=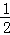 ,满足题意;…(7分)
,满足题意;…(7分)
( ii)b>0时,b•12﹣2•1+1<0,即0<b<1;…(8分)
( iii)b<0时,b•12﹣2•1+1<0,得b<1,故b<0;
综上所述,得:h(x)在(0,1)上有且只有一个极值点时,b<1. …(9分)
(3)证明:由(1)可知:
( i)若a≤0,则f'(x)≥0,f(x)在(0,+∞)上为单调增函数,
所以直线l与y=F(x)的图象不可能有两个切点,不合题意.…(10分)
(ⅱ)若a>0,f(x)在x=a处取得极值f(a)=1+lna.
若1+lna≥0,a≥ 时,由图象知不可能有两个切点.…(11分)
时,由图象知不可能有两个切点.…(11分)
故0<a< ,设f(x)图象与x轴的两个切点的横坐标为s,t(不妨设s<t),
,设f(x)图象与x轴的两个切点的横坐标为s,t(不妨设s<t),
则直线l与y=F(x)的图象有两个切点即为直线l与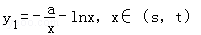
和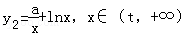 的切点.
的切点.
y1'=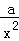 ﹣
﹣ =
=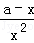 ,y2'=﹣
,y2'=﹣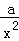 +
+ =
=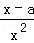 ,
,
设切点分别为A(x1,y1),B(x2,y2),则0<x1<x2,且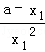 =
=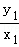 =﹣
=﹣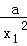 ﹣
﹣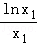 ,
,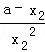 =
=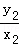 =
=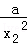 +
+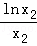 ,
,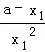 =
=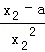 ,
,
即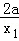 =1﹣lnx1…①;
=1﹣lnx1…①;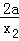 =1﹣lnx2…②;a=
=1﹣lnx2…②;a=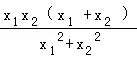 ,③
,③
①﹣②得: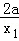 ﹣
﹣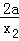 =﹣lnx1+lnx2=﹣ln
=﹣lnx1+lnx2=﹣ln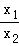 ,
,
由③中的a代入上式可得:(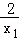 ﹣
﹣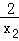 )•
)•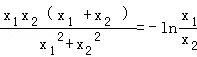 ,
,
即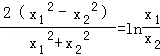 ,…(14分)
,…(14分)
令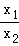 =k(0<k<1),则(k2+1)lnk=2k2﹣2,令G(k)=(k2+1)lnk﹣2k2+2,(0<k<1),
=k(0<k<1),则(k2+1)lnk=2k2﹣2,令G(k)=(k2+1)lnk﹣2k2+2,(0<k<1),
因为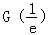 =1﹣
=1﹣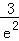 >0,
>0,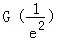 =﹣
=﹣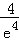 <0,
<0,
故存在k0∈(0,1),使得G(k0)=0,
即存在一条过原点的直线l与y=F(x)的图象有两个切点.…(16分)
考点:利用导数研究函数的单调性;函数在某点取得极值的条件;利用导数研究曲线上某点切线方程
点评:本题给出含有分式和对数的基本初等函数,求函数f(x)的单调区间、讨论函数f(x)+g(x)的极值点并证明了函数|f(x)|图象与过原点的直线相切的问题.着重考查了基本初等函数的性质、利用导数研究函数的单调性、直线的斜率公式和用导数求函数图象的切线等知识,属于难题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的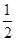 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数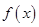 .
.
⑴试规定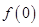 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数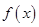 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设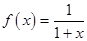 ,现有
,现有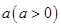 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数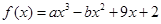 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的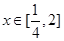 ,都有f(x)
,都有f(x)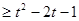 成立,求函数g(t)
成立,求函数g(t)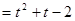 的最值
的最值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用 万元满足
万元满足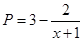 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本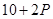 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为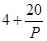 元.
元.
(Ⅰ)将该产品的利润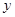 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电 度时,应缴电费
度时,应缴电费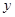 元,写出
元,写出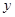 关于
关于 的函数关系式;
的函数关系式;
(2)小明家第一季度缴纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 缴费金额 | 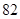 元 元 | 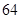 元 元 | 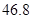 元 元 | 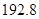 元 元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com