
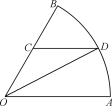
����Ŀ����ͼ��һ���뾶Ϊ2ǧ�ף�Բ�Ľ�Ϊ![]() ��������������ƽ��ʾ��ͼ
��������������ƽ��ʾ��ͼ![]() �ǰ뾶
�ǰ뾶![]() ��һ�㣬
��һ�㣬![]() ��Բ��
��Բ��![]() ��һ�㣬��
��һ�㣬��![]() .�����߶�
.�����߶�![]() ���߶�
���߶�![]() ��Բ��
��Բ��![]() ������ʾλ���������λ����������λ���������ǣ��߶�
������ʾλ���������λ����������λ���������ǣ��߶�![]() ��ÿǧ��Ϊ
��ÿǧ��Ϊ![]() Ԫ���߶�
Ԫ���߶�![]() ��Բ��
��Բ��![]() ��ÿǧ��Ϊ
��ÿǧ��Ϊ![]() Ԫ����
Ԫ����![]() ���ȣ����λ�����������Ϊ
���ȣ����λ�����������Ϊ![]() Ԫ��
Ԫ��
(1)��![]() ����
����![]() �ĺ�������ʽ����ָ���ú����Ķ�����
�ĺ�������ʽ����ָ���ú����Ķ�����
(2)���ʣ�![]() Ϊ��ֵʱ�����λ����������������������ֵ��
Ϊ��ֵʱ�����λ����������������������ֵ��
���𰸡���1��![]() ����2����
����2����![]() ʱ�����λ�����������������ֵΪ
ʱ�����λ�����������������ֵΪ![]() Ԫ.
Ԫ.
��������
��1���������⣬�������Ҷ������OC��ֵ������DB���������y�Ľ���ʽ��д��x��ȡֵ��Χ��
��2������y�ĵ��������õ����жϺ����ĵ����ԣ������������ֵ�Ͷ�Ӧx��ֵ��
(1)��Ϊ![]() ������
������![]() .
.
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�����Ҷ�������![]() ��
��
��![]() ��
��![]() .
.
��Բ��![]() ��Ϊ
��Ϊ![]() ��
��
����![]()
![]() .
.
(2)��![]() ��
��
��![]() ��
��
��![]() ����
����![]() .
.
��![]() �仯ʱ��
�仯ʱ��![]() ��
��![]() �ı仯���±���
�ı仯���±���
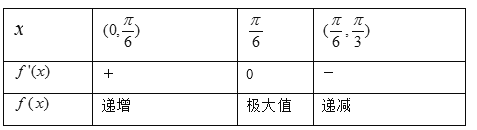
����![]() ��
��![]() ��ȡ�ü���ֵ���������ֵ�������ֵ����
��ȡ�ü���ֵ���������ֵ�������ֵ����![]() .
.
�ʵ�![]() ʱ�����λ�����������������ֵΪ
ʱ�����λ�����������������ֵΪ![]() Ԫ��
Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ����
����![]() ��������Ϊ
��������Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2��![]() ��
�� ![]() �ǹ���
�ǹ���![]() �һ��ഹֱ������ֱ�ߣ�����
�һ��ഹֱ������ֱ�ߣ�����![]() ��Բ
��Բ![]() ��
��![]() ��
�� ![]() ���㣬
���㣬 ![]() ����Բ
����Բ![]() ����һ����
����һ����![]() ����
����![]() ���ȡ�����ֵʱֱ��
���ȡ�����ֵʱֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���豸����ʹ���������ӣ�ÿ���ά������Ӧ����![]() �ֶ�һ�����豸���е��飬�õ������豸�Թ���ʹ��֮����ǰ����ƽ��ÿ̨�豸ÿ���ά�����ô��������
�ֶ�һ�����豸���е��飬�õ������豸�Թ���ʹ��֮����ǰ����ƽ��ÿ̨�豸ÿ���ά�����ô��������
��� | 1 | 2 | 3 | 4 | 5 |
���� |
|
|
|
|
|
![]() ��
��![]() ��y����t�����Իع鷽�̣�
��y����t�����Իع鷽�̣�
![]() ��
��![]() �����豸�ļ۸���ÿ̨5��Ԫ������ΪӦ��ʹ�������껻һ���豸����������ΪӦ��ʹ����ʮ�껻һ���豸������Ϊ����˭���е�������˵�����ɣ�
�����豸�ļ۸���ÿ̨5��Ԫ������ΪӦ��ʹ�������껻һ���豸����������ΪӦ��ʹ����ʮ�껻һ���豸������Ϊ����˭���е�������˵�����ɣ�
![]() �ο���ʽ��
�ο���ʽ�� ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��t��1��Ϊ����y��ax2+bx+4��a��bΪ��������a��0����y��xͼ��Ľ��㣮
��1����t��
��2��������y��ax2+bx+4��ͼ����x��ֻ��һ�����㣬��a��b��
��3����1��a��2���赱![]() ��x��2ʱ������y��ax2+bx+4�����ֵΪm����СֵΪn����m��n����Сֵ��
��x��2ʱ������y��ax2+bx+4�����ֵΪm����СֵΪn����m��n����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1��������![]() ��
��![]() �ϵ����ݼ�����ʵ��
�ϵ����ݼ�����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() ��
��![]() �ϵ�ֵ��ǡ����
�ϵ�ֵ��ǡ����![]() �������ڣ����ʵ��
�������ڣ����ʵ��![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ2017��Ĵ�����Ϊ500��Ԫ�����豸�ϻ���ԭ����ҵ���������������½��������ܽ��м������죬Ԥ���2018����ÿ�����һ�괿�������20��Ԫ��2018�������ҵһ����Ͷ���ʽ�600��Ԫ���м������죬Ԥ����δ�۳����������ʽ������£���![]() �꣨��2018��Ϊ��һ�꣩������Ϊ
�꣨��2018��Ϊ��һ�꣩������Ϊ![]() ��Ԫ��
��Ԫ��![]() Ϊ��������.
��������.
��1����ӽ������ǰ![]() �꣬������ҵ�����м���������ۼ�������Ϊ
�꣬������ҵ�����м���������ۼ�������Ϊ![]() ��Ԫ�����м����������ۼƴ�����Ϊ
��Ԫ�����м����������ۼƴ�����Ϊ![]() ��Ԫ����۳����������ʽ𣩣���
��Ԫ����۳����������ʽ𣩣���![]() ��
��![]() �ı���ʽ��
�ı���ʽ��
��2��������Ԥ�⣬��2018�������ҵ���پ��������꣬���м����������ۼ����������м���������ۼƴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��![]() ��������
��������
��1��������![]() �뺯��
�뺯��![]() ��
��![]() ������ͬ�����ߣ���ʵ��
������ͬ�����ߣ���ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ����
����![]() ��֤����
��֤���� ![]() ��
��
��3����������![]() ������ʽ��
������ʽ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��x0��y0����x0��![]() ������ԲC��
������ԲC��![]() ��a��b��0���ϣ�����MΪ��ԲC���Ҷ��㣬��PO��PM ��OΪ����ԭ�㣩������ԲC��������e��ȡֵ��Χ��
��a��b��0���ϣ�����MΪ��ԲC���Ҷ��㣬��PO��PM ��OΪ����ԭ�㣩������ԲC��������e��ȡֵ��Χ��
A. ��0��![]() �� B. ��0��1�� C. ��
�� B. ��0��1�� C. ��![]() ��1�� D. ��0��
��1�� D. ��0��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com