
已知函数![]() 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义:
![]() ,
,![]() ,其中
,其中![]() 表示函数
表示函数![]() 在D上的最小值,
在D上的最小值,![]() 表示函数
表示函数![]() 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若![]() ,试写出
,试写出![]() ,
,![]() 的表达式;
的表达式;
(2)已知函数![]() 试判断
试判断![]() 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
(3)已知![]() ,函数
,函数![]() 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
解:(1)由题意可得:![]() ,
,![]() 。
。
(2)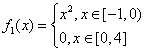 ,
,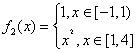 ,
,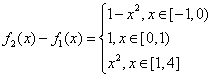
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
综上所述,![]() 。
。
即存在![]() ,使得
,使得![]() 是[-1,4]上的“4阶收缩函数”。
是[-1,4]上的“4阶收缩函数”。
(3)![]() ,令
,令![]() 得
得![]() 或
或![]() 。
。
函数![]() 的变化情况如下:
的变化情况如下:
| x |
| 0 |
| 2 |
|
|
| - | 0 | + | 0 | - |
|
|
| 0 |
| 4 |
|
令![]() 得
得![]() 或
或![]() 。
。
(i)当![]() 时,
时,![]() 在
在![]() 上单调递增,因此,
上单调递增,因此,![]() ,
,![]() 。因为
。因为![]() 是
是![]() 上的“二阶收缩函数”,所以,
上的“二阶收缩函数”,所以,
①![]() 对
对![]() 恒成立;
恒成立;
②存在![]() ,使得
,使得![]() 成立。
成立。
①即:![]() 对
对![]() 恒成立,由
恒成立,由![]() 解得
解得![]() 或
或![]() 。
。
要使![]() 对
对![]() 恒成立,需且只需
恒成立,需且只需![]() 。
。
②即:存在![]() ,使得
,使得![]() 成立。
成立。
由![]() 解得
解得![]() 或
或![]() 。
。
所以,只需![]() 。
。
综合①②可得![]() 。
。
(i i)当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,因此,
上单调递减,因此,![]() ,
,![]() ,
,![]() ,显然当
,显然当![]() 时,
时,![]() 不成立。
不成立。
(i i i)当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,因此,
上单调递减,因此,![]() ,
,![]() ,
,![]() ,显然当
,显然当![]() 时,
时,![]() 不成立。
不成立。
综合(i)(i i)(i i i)可得:![]() 。
。


科目:高中数学 来源:2013-2014学年福建福州一中高三上学期期末考试文科数学试卷(解析版) 题型:解答题
已知函数 的图像在点
的图像在点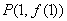 处的切线斜率为10.
处的切线斜率为10.
(1)求实数 的值;
的值;
(2)判断方程 根的个数,并证明你的结论;
根的个数,并证明你的结论;
(21)探究: 是否存在这样的点 ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三上学期期末质量检测文科数学试卷(解析版) 题型:选择题
已知函数 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列 的前n项和为
的前n项和为 ,则S2013的值为( )
,则S2013的值为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三2月月考数学理卷 题型:解答题
(本小题14分)
已知函数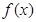 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义:
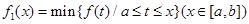 ,
, ,其中
,其中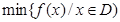 表示函数
表示函数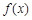 在D上的最小值,
在D上的最小值, 表示函数
表示函数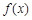 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得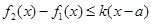 对任意的
对任意的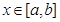 成立,则称函数
成立,则称函数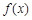 为
为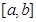 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若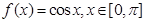 ,试写出
,试写出 ,
,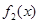 的表达式;
的表达式;
(2)已知函数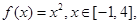 试判断
试判断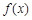 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
已知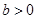 ,函数
,函数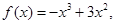 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三2月月考数学理卷 题型:解答题
(本小题14分)
已知函数 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义:
 ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 为
为 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若 ,试写出
,试写出 ,
, 的表达式;
的表达式;
(2)已知函数 试判断
试判断 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
已知 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com