Question

9．在平面内，定点A，B，C，D满足$|\overrightarrow{DA}|$=$|\overrightarrow{DB}|$=$|\overrightarrow{DC}|$，$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=$\overrightarrow{DC}$•$\overrightarrow{DA}$=-2，动点P，M满足$|\overrightarrow{AP}|$=1，$\overrightarrow{PM}$=$\overrightarrow{MC}$，则|$\overrightarrow{BM}$|²的最大值是（　　）

• A． $\frac{43}{4}$
• B． $\frac{49}{4}$
• C． $\frac{37+6\sqrt{3}}{4}$
• D． $\frac{37+2\sqrt{33}}{4}$

Answer 1

分析 由$|\overrightarrow{DA}|$=$|\overrightarrow{DB}|$=$|\overrightarrow{DC}|$，可得D为△ABC的外心，又$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=$\overrightarrow{DC}$•$\overrightarrow{DA}$，可得可得D为△ABC的垂心，则D为△ABC的中心，即△ABC为正三角形．运用向量的数量积定义可得△ABC的边长，以A为坐标原点，AD所在直线为x轴建立直角坐标系xOy，求得B，C的坐标，再设P（cosθ，sinθ），（0≤θ＜2π），由中点坐标公式可得M的坐标，运用两点的距离公式可得BM的长，运用三角函数的恒等变换公式，结合正弦函数的值域，即可得到最大值．

解答 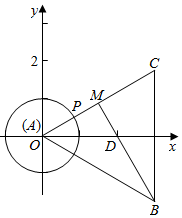解：由$|\overrightarrow{DA}|$=$|\overrightarrow{DB}|$=$|\overrightarrow{DC}|$，可得D为△ABC的外心，
又$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=$\overrightarrow{DC}$•$\overrightarrow{DA}$，可得
$\overrightarrow{DB}$•（$\overrightarrow{DA}$-$\overrightarrow{DC}$）=0，$\overrightarrow{DC}$•（$\overrightarrow{DB}$-$\overrightarrow{DA}$）=0，
即$\overrightarrow{DB}$•$\overrightarrow{AC}$=$\overrightarrow{DC}$•$\overrightarrow{AB}$=0，
即有$\overrightarrow{DB}$⊥$\overrightarrow{AC}$，$\overrightarrow{DC}$⊥$\overrightarrow{AB}$，可得D为△ABC的垂心，
则D为△ABC的中心，即△ABC为正三角形．
由$\overrightarrow{DA}$•$\overrightarrow{DB}$=-2，即有|$\overrightarrow{DA}$|•|$\overrightarrow{DA}$|cos120°=-2，
解得|$\overrightarrow{DA}$|=2，△ABC的边长为4cos30°=2$\sqrt{3}$，
以A为坐标原点，AD所在直线为x轴建立直角坐标系xOy，
可得B（3，-$\sqrt{3}$），C（3，$\sqrt{3}$），D（2，0），
由$|\overrightarrow{AP}|$=1，可设P（cosθ，sinθ），（0≤θ＜2π），
由$\overrightarrow{PM}$=$\overrightarrow{MC}$，可得M为PC的中点，即有M（$\frac{3+cosθ}{2}$，$\frac{\sqrt{3}+sinθ}{2}$），
则|$\overrightarrow{BM}$|²=（3-$\frac{3+cosθ}{2}$）²+（$\frac{\sqrt{3}+sinθ}{2}$+$\sqrt{3}$）²
=$\frac{（3-cosθ）^{2}}{4}$+$\frac{（3\sqrt{3}+sinθ）^{2}}{4}$=$\frac{37-6cosθ+6\sqrt{3}sinθ}{4}$
=$\frac{37+12sin（θ-\frac{π}{6}）}{4}$，
当sin（θ-$\frac{π}{6}$）=1，即θ=$\frac{2π}{3}$时，取得最大值，且为$\frac{49}{4}$．
故选：B．

点评 本题考查向量的定义和性质，以及模的最值的求法，注意运用坐标法，转化为三角函数的最值的求法，考查化简整理的运算能力，属于中档题．