练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图K41­7所示，正方体ABCD ­ A1B1C1D1中，A1C与截面DBC1交于O点，AC，BD交于M点，求证：C1，O，M三点共线．

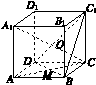
    图K41­7


    证明：连接C1M，∵C1∈平面A1ACC1，且C1∈平面DBC1，

    ∴C1是平面A1ACC1与平面DBC1的公共点．

    又∵M∈AC，∴M∈平面A1ACC1.

    ∵M∈BD，∴M∈平面DBC1，

    ∴M也是平面A1ACC1与平面DBC1的公共点，

    ∴C1M是平面A1ACC1与平面DBC1的交线．

    ∵O为A1C与截面DBC1的交点，

    ∴O∈平面A1ACC1，O∈平面DBC1，

    即O也是两平面的公共点，

    ∴O∈直线C1M，即C1，O，M三点共线．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知点P(x0，y0)，圆O：x2＋y2＝r2(r＞0)，直线l：x0x＋y0y＝r2，有以下几个结论：①若点P在圆O上，则直线l与圆O相切；②若点P在圆O外，则直线l与圆O相离；③若点P在圆O内，则直线l与圆O相交；④无论点P在何处，直线l与圆O恒相切．其中正确结论的个数是(　　)

    A．1  B．2

    C．3  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3(n∈N*)能被9整除”，要利用归纳假设证当n＝k＋1时的情况，只需展开(　　)

    A．(k＋3)3  B．(k＋2)3

    C．(k＋1)3  D．(k＋1)3＋(k＋2)3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A，B，C，D是空间内四个不同的点，在下列结论中，不正确的是(　　)

    A．若AC与BD共面，则AD与BC共面

    B．若AC与BD是异面直线，则AD与BC是异面直线

    C．若AB＝AC，DB＝DC，则AD＝BC

    D．若AB＝AC，DB＝DC，则AD⊥BC

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c为三条不同的直线，且a⊂平面α，b⊂平面β，α∩β＝c.给出下列命题：

    ①若a与b是异面直线，则c至少与a，b中的一条相交；

    ②若a不垂直于c，则a与b一定不垂直；

    ③若a∥b，则必有a∥c；

    ④若a⊥b，a⊥c，则必有α⊥β.

    其中真命题的个数是(　　)

    A．0  B．1 

    C．2  D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个几何体的三视图及其尺寸如图K40­5所示(单位：cm)，其中主视图是直角三角形，左视图是半圆，俯视图是等腰三角形，则这个几何体的体积是(　　)

    　D．π cm

    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若某几何体的三视图(单位：cm)如图K40­12所示，则此几何体的体积等于________ cm3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图K42­2所示，正方体ABCD ­ A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


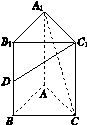
    如图K45­3所示，直三棱柱ABC ­ A1B1C1中，AB＝AC＝1，AA1＝2，∠B1A1C1＝90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为________．

    查看答案和解析>>

    同步练习册答案