
 2016年入冬以来,各地雾霾天气频发,PM2.5频频爆表(PM2.5是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与PM2.5的浓度是否相关,某市现采集到周一到周五某一时间段车流量与PM2.5的数据如表:
2016年入冬以来,各地雾霾天气频发,PM2.5频频爆表(PM2.5是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与PM2.5的浓度是否相关,某市现采集到周一到周五某一时间段车流量与PM2.5的数据如表:| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
分析 (1)根据表中数据画出散点图即可;
(2)散点图中各点分布在一条直线附近,判断x与y是有线性关系;计算$\overline{x}$、$\overline{y}$,求出回归系数,写出线性回归方程.
解答 解:(1)根据上述数据,画出散点图如图所示: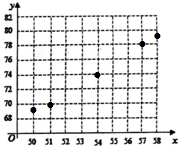
(2)散点图中各点成线状分布,判断x与y是有线性关系,
根据表中数据,计算$\overline{x}$=$\frac{1}{5}$×(50+51+54+57+58)=54,
$\overline{y}$=$\frac{1}{5}$×(69+70+74+78+79)=74,
$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=(-4)×(-5)+(-3)×(-4)+0×0+3×4+4×5=64,
$\sum_{i=1}^{5}$${{(x}_{i}-\overline{x})}^{2}$=(-4)2+(-3)2+02+32+42=50,
∴$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{64}{50}$=1.28,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=74-1.28×54=4.88;
∴y关于x的线性回归方程为$\stackrel{∧}{y}$=1.28x+4.88.
点评 本题考查了线性回归方程的求法与应用问题,是基础题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,其中俯视图是半圆里面内切一个小圆,若该几何体的表面积为16+16π,则正视图中的a值为( )
某几何体的三视图如图所示,其中俯视图是半圆里面内切一个小圆,若该几何体的表面积为16+16π,则正视图中的a值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 41 | C. | 82 | D. | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com