
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD= ![]() AD.
AD. 
(1)求证:平面PAB⊥平面PDC
(2)在线段AB上是否存在一点G,使得二面角C﹣PD﹣G的余弦值为 ![]() .若存在,求
.若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(1)证明:∵AD=2,∴ ![]() ,
,
∴PA2+PD2=AD2∴PD⊥AP,
又∵平面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥平面PAD,又PD平面PAD,∴AB⊥PD,
又∵AP∩AP=A,且AP、AB平面PAB,
∴PD⊥平面PAB,
又PD平面PDC,∴平面PAB⊥平面PDC
(2)解:如图,取AD的中点O,连接OP,OF,
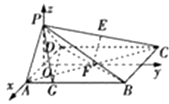
∵PA=PD,∴PO⊥AD.
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD,
而O,F分别为AD,BD的中点,∴OF∥AB,
又ABCD是正方形,∴OF⊥AD,
以O为原点,射线OA,OF,OP为x轴,y轴,z轴建立空间直角坐标系O﹣xyz,
则有A(1,0,0),C(﹣1,2,0),F(0,1,0),D(﹣1,0,0),P(0,0,1),
若在AB上存在点G,使得二面角C﹣PD﹣G的余弦值为 ![]() ,连接PG、DG,
,连接PG、DG,
设G(1,a,0)(0≤a≤2),
则 ![]() =(1,0,1),
=(1,0,1), ![]() =(﹣2,﹣a,0),
=(﹣2,﹣a,0),
由(2)知平面PDC的一个法向量为 ![]() =(1,0,﹣1),
=(1,0,﹣1),
设平面PGD的法向量为 ![]() =(x,y,z).
=(x,y,z).
则 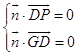 ,即
,即 ![]() ,.
,.
令y=﹣2,得 ![]() =(a,﹣2,﹣a),
=(a,﹣2,﹣a),
∴|cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() ,解得a=
,解得a= ![]() ,
,
∴a= ![]() ,此时
,此时 ![]() ,
,
∴在线段AB上存在点G(1, ![]() ,0)使得二面角C﹣PD﹣G的余弦值为
,0)使得二面角C﹣PD﹣G的余弦值为 ![]() ,
, ![]() .
.
【解析】(1)推导出PD⊥AP,AB⊥PD,由此能证明平面PAB⊥平面PDC.(2)取AD的中点O,连接OP,OF,PO⊥AD,以O为原点,射线OA,OF,OP为x轴,y轴,z轴建立空间直角坐标系O﹣xyz,由此利用向量法能求出在线段AB上存在点G(1, ![]() ,0)使得二面角C﹣PD﹣G的余弦值为
,0)使得二面角C﹣PD﹣G的余弦值为 ![]() ,
, ![]() .
.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分10分)如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 在线段
在线段![]() 上(点
上(点![]() 与点
与点![]() 不重合).
不重合).

(1)若异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的长度;
的长度;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】射击测试有两种方案,方案1:先在甲靶射击一次,以后都在乙靶射击;方案2:始终在乙靶射击,某射手命中甲靶的概率为![]() ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为![]() ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量![]() 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果![]() 的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
(1)如果该射手选择方案1,求其测试结束后所得分![]() 的分布列和数学期望E
的分布列和数学期望E![]() ;
;
(2)该射手选择哪种方案通过测试的可能性大?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解学生对周末家庭作业量的态度,拟采用分层抽样的方法分别从高一、高二、高三的高中生中随机抽取一个容量为200的样本进行调查,已知从700名高一、高二学生中共抽取了140名学生,那么该校有高三学生名.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知抛物线![]() 的焦点为
的焦点为![]() ,
, ![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为
的横坐标为![]() 时,
时, ![]() 为正三角形.
为正三角形.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和
和![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,
(ⅰ)证明直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(ⅱ)![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2sinx,﹣cosx)、B( ![]() cosx,2cosx),记f(x)=
cosx,2cosx),记f(x)= ![]()
![]() .
.
(1)若x0是函数y=f(x)﹣1的零点,求tanx0的值;
(2)求f(x)在区间[ ![]() ,
, ![]() ]上的最值及对应的x的值.
]上的最值及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 满足
满足![]() ,且在定义域内
,且在定义域内![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosωx(sinωx+ ![]() cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 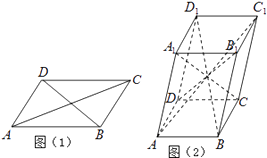
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com