考点:平面与平面平行的判定,直线与平面平行的判定
专题:空间位置关系与距离
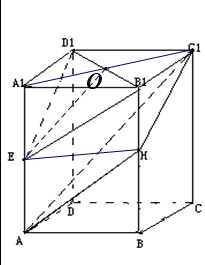
分析:(1)连A1C1,A1C1交B1D1与点O,根据直线与平面平行的判定定理即可证明AC1∥平面EB1D1.
(2)首先利用直线与平面平行的判定定理证明HC1∥平面EB1D1.再由(1)知AC1∥平面EB1D1.利用平面与平面平行的判定定理即可得到平面EB1D1∥平面AHC1
解答:
证明:(1)连A
1C
1,A
1C
1交B
1D
1与点O,
∵四边形A
1B
1C
1D
1为平行四边形,
则点O是A
1C
1的中点,
又∵E是AA
1的中点,
∴EO是△AA
1C
1的中位线,
∴EO∥AC
1又∵AC
1?面EB
1D
1,EO?面EB
1D
1,
∴AC
1∥平面EB
1D
1.
(2)连接EH,
∵E,H分别是AA
1、BB
1的中点
则EH∥A
1B
1.且EH=A
1B
1.
又∵A
1B
1∥C
1D
1,且A
1B
1=C
1D
1,
∴EH∥C
1D
1,且EH=C
1D
1.
∴四边形EHC
1D
1是平行四边形.
∴ED
1∥HC
1.
又∵ED
1?平面EB
1D
1,HC
1?平面EB
1D
1,
∴HC
1∥平面EB
1D
1.
由(1)知,AC
1∥平面EB
1D
1,
∵AC
1∩HC
1=C
1,
∴平面EB
1D
1∥平面AHC
1.
点评:本题考查直线与平面平行以及平面与平面平行的判定定理.属于中档题.

 如图,在平行六面体ABCD-A1B1C1D1中,E,H分别是AA1、BB1的中点,求证:
如图,在平行六面体ABCD-A1B1C1D1中,E,H分别是AA1、BB1的中点,求证:


 名校课堂系列答案
名校课堂系列答案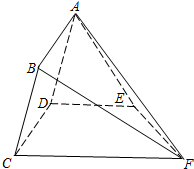 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3