练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （2011•安徽模拟）已知函数f（x）的导函数为f′（x），且满足f（x）=2xf′（1）+lnx，则f′（1）=（ ）

    A.﹣e B.﹣1 C.1 D.e

    B

    【解析】

    试题分析：已知函数f（x）的导函数为f′（x），利用求导公式对f（x）进行求导，再把x=1代入，即可求解；

    【解析】
    ∵函数f（x）的导函数为f′（x），且满足f（x）=2xf′（1）+ln x，（x＞0）

    ∴f′（x）=2f′（1）+，把x=1代入f′（x）可得f′（1）=2f′（1）+1，

    解得f′（1）=﹣1，

    故选B；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系（解析版） 题型：填空题

    （2011•成都二模）如图，在半径为l的球O中．AB、CD是两条互相垂直的直径，半径OP⊥平面ACBD．点E、F分别为大圆上的劣弧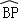、的中点，给出下列结论：

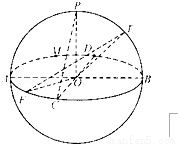
    ①E、F两点的球面距离为；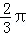

    ②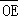向量在向量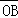方向上的投影恰为；

    ③若点M为大圆上的劣弧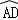的中点，则过点M且与直线EF、PC成等角的直线有无数条；

    ④球面上到E、F两点等距离的点的轨迹是两个点；

    其中你认为正确的所有结论的序号为 ．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷（解析版） 题型：?????

    下列求导运算正确的是（ ）

    A.

    B.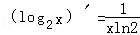

    C.（（2x+3）2）′=2（2x+3）

    D.（e2x）′=e2x

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷（解析版） 题型：?????

    （2014•榆林模拟）要得到函数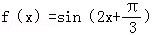的导函数f′（x）的图象，只需将f（x）的图象（ ）

    A.向右平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）

    B.向左平移个单位，再把各点的纵坐标缩短到原来的2倍（横坐标不变）

    C.向右平移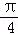个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）

    D.向左平移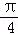个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷（解析版） 题型：?????

    已知函数f（x）的导函数为f′（x），且满足关系式f（x）=x2+3xf′（2）+lnx，则f′（2）的值等于（ ）

    A.2 B.﹣2 C. D.

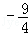
    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷（解析版） 题型：?????

    （2013•绵阳一模）己知f（x）=xsinx，则f′（π）=（ ）

    A.O B.﹣1 C.π D.﹣π

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷（解析版） 题型：?????

    平面α的一个法向量=（1，﹣1，0），则y轴与平面α所成的角的大小为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷（解析版） 题型：填空题

    已知点A（3，﹣2，1），B（﹣2，4，0），则向量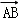的坐标为 ．

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷（解析版） 题型：填空题

    若非零向量，满足，则，的夹角的大小为__________．

    查看答案和解析>>

    同步练习册答案