
(2013•绵阳一模)己知f(x)=xsinx,则f′(π)=( )
A.O B.﹣1 C.π D.﹣π
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°,则该截面的面积是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
函数y=sin(2x2+x)导数是( )
A.y′=cos(2x2+x)
B.y′=2xsin(2x2+x)
C.y′=(4x+1)cos(2x2+x)
D.y′=4cos(2x2+x)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
设函数f(x)= (sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )
(sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )
A.f′(x)+f(x)=﹣sinx B.f′(x)+f(x)=﹣cosx
C.f′(x)﹣f(x)=sinx D.f′(x)﹣f(x)=cosx
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2011•安徽模拟)已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(1)=( )
A.﹣e B.﹣1 C.1 D.e
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD中点,则∠AED的大小为( )
A.45° B.30° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
若向量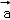 =(1,λ,2),
=(1,λ,2),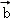 =(﹣2,1,1),
=(﹣2,1,1),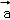 ,
,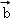 夹角的余弦值为
夹角的余弦值为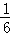 ,则λ等于( )
,则λ等于( )
A.1 B.﹣1 C.±1 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷(解析版) 题型:选择题
已知{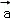 ,
,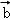 ,
,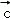 }是空间的一组单位正交基底,而{
}是空间的一组单位正交基底,而{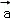 ﹣
﹣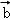 ,
,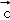 ,
, +
+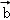 }是空间的另一组基底.若向量
}是空间的另一组基底.若向量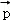 在基底{
在基底{ ,
,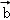 ,
,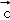 }下的坐标为(6,4,2),则向量
}下的坐标为(6,4,2),则向量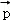 在基底{
在基底{ ﹣
﹣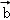 ,
,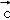 ,
,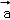 +
+ }下的坐标为( )
}下的坐标为( )
A.(1,2,5) B.(5,2,1) C.(1,2,3) D.(3,2,1)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:选择题
若关于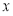 的方程
的方程 在区间
在区间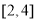 上有实数根,则实数
上有实数根,则实数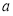 的取值范围是( )
的取值范围是( )
(A)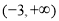 (B)
(B)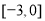 (C)
(C)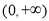 (D)
(D)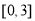
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com