
将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD中点,则∠AED的大小为( )
A.45° B.30° C.60° D.90°
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
过球面上两点可能作出的球的大圆( )
A.0个或1个 B.有且仅有1个 C.无数个 D.一个或无数个
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
设函数f(x)=g(x)+x+lnx,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处的切线方程为( )
A.y=4x B.y=4x﹣8 C.y=2x+2 D.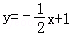
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2013•绵阳一模)己知f(x)=xsinx,则f′(π)=( )
A.O B.﹣1 C.π D.﹣π
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
ABCD是正方形,PA⊥平面AC,且PA=AB,则二面角B﹣PC﹣D的度数为( )
A.60° B.90° C.120° D.135°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
在长方体ABCD﹣A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为( )
A. B.
B.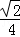 C.
C.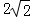 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数 ,
,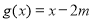 ,其中
,其中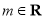 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当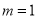 时,求函数
时,求函数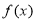 的极小值;
的极小值;
(Ⅱ)对 ,是否存在
,是否存在 ,使得
,使得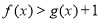 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)设 ,当
,当 时,若函数
时,若函数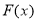 存在
存在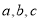 三个零点,且
三个零点,且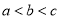 ,求证:
,求证:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com