
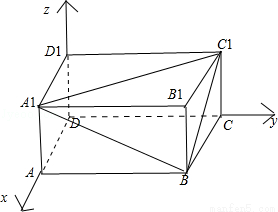
在长方体ABCD﹣A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为( )
A. B.
B.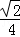 C.
C.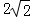 D.
D.
A
【解析】
试题分析:可以考虑用向量解决本题,所以分别以DA,DC,DD1三直线为x轴,y轴,z轴建立空间直角坐标系,根据线面角的概念知D1C1与平面A1BC1所成角的正弦值等于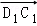 与平面A1BC1的法向量夹角的余弦值的绝对值,所以根据已知的边的长度求出
与平面A1BC1的法向量夹角的余弦值的绝对值,所以根据已知的边的长度求出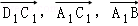 的坐标,设平面A1BC1的法向量为
的坐标,设平面A1BC1的法向量为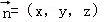 ,根据向量
,根据向量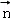 与
与 垂直即可求出
垂直即可求出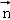 ,根据向量夹角余弦公式即可求出向量
,根据向量夹角余弦公式即可求出向量 ,
,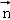 夹角的余弦值的绝对值.
夹角的余弦值的绝对值.
【解析】
如图,分别以DA,DC,DD1三条边所在直线为x轴,y轴,z轴建立空间直角坐标系;
根据题意知,D1C1与平面A1BC1所成角的正弦值等于向量 和平面A1BC1的法向量夹角余弦值的绝对值;
和平面A1BC1的法向量夹角余弦值的绝对值;
根据已知的边的长度,可求以下几点坐标:
D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0);
∴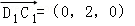 ,
,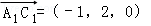 ,
,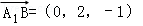 ;
;
设平面A1BC1的法向量为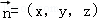 ,则
,则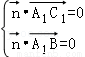 ;
;
∴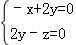 ,取y=1,∴
,取y=1,∴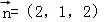 ;
;
∴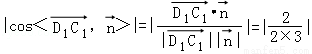 =
= .
.
故选A.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某批产品共10件,已知从该批产品中任取1件,则取到的是次品的概率为P=0.2.若从该批产品中任意抽取3件,
(1)求取出的3件产品中恰好有一件次品的概率;
(2)求取出的3件产品中次品的件数X的概率分布列与期望.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
设函数f(x)= (sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )
(sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )
A.f′(x)+f(x)=﹣sinx B.f′(x)+f(x)=﹣cosx
C.f′(x)﹣f(x)=sinx D.f′(x)﹣f(x)=cosx
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD中点,则∠AED的大小为( )
A.45° B.30° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
若向量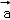 =(1,λ,2),
=(1,λ,2),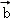 =(﹣2,1,1),
=(﹣2,1,1),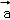 ,
,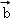 夹角的余弦值为
夹角的余弦值为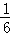 ,则λ等于( )
,则λ等于( )
A.1 B.﹣1 C.±1 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
(2012•静安区一模)在棱长为1的正方体ABCD﹣A1B1C1D1中,E为棱BC的中点,F为棱DD1的中点.则异面直线EF与BD1所成角的余弦值是( )
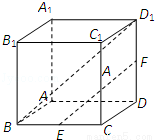
A.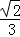 B.
B.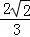 C.
C.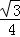 D.
D.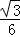
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷(解析版) 题型:选择题
已知{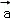 ,
,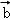 ,
,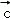 }是空间的一组单位正交基底,而{
}是空间的一组单位正交基底,而{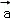 ﹣
﹣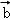 ,
,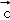 ,
, +
+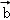 }是空间的另一组基底.若向量
}是空间的另一组基底.若向量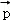 在基底{
在基底{ ,
,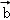 ,
,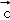 }下的坐标为(6,4,2),则向量
}下的坐标为(6,4,2),则向量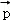 在基底{
在基底{ ﹣
﹣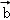 ,
,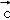 ,
,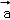 +
+ }下的坐标为( )
}下的坐标为( )
A.(1,2,5) B.(5,2,1) C.(1,2,3) D.(3,2,1)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:选择题
已知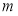 ,
,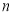 是两条不同直线,
是两条不同直线,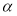 ,
,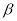 是两个不同的平面,且
是两个不同的平面,且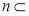
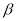 ,则下列叙述正确的是
,则下列叙述正确的是
(A)若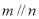 ,
,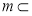
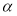 ,则
,则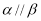
(B)若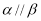 ,
,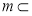
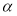 ,则
,则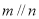
(C)若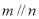 ,
,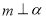 ,则
,则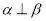
(D)若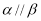 ,
,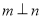 ,则
,则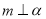
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:填空题
一副扑克牌(有四色,同一色有13张不同牌)共52张.现随机抽取3张牌,则抽出的3张牌有且仅有2张花色相同的概率为 (用数值作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com