
ABCD是正方形,PA⊥平面AC,且PA=AB,则二面角B﹣PC﹣D的度数为( )
A.60° B.90° C.120° D.135°
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
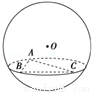
(2009•四川)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
A.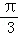 B.π C.
B.π C.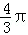 D.2π
D.2π
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
(2012•德阳三模)已知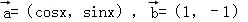 ,将函数
,将函数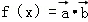 的图象按向量
的图象按向量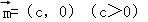 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
A.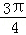 B.π C.
B.π C.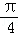 D.
D.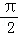
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2012•赣州模拟)函数f(x)=ax3+bx2+cx+d(a≠0),若a+b+c=0,导函数f′(x)满足f′(0)f′(1)>0,设f′(x)=0的两根为x1,x2,则|x1﹣x2|的取值范围是( )
A.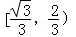 B.
B.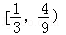 C.
C.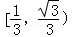 D.
D.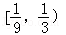
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD中点,则∠AED的大小为( )
A.45° B.30° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
在空间中,“经过点P(x0,y0,z0),法向量为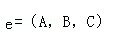 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是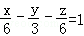 ,则由这两平面所成的二面角的正弦值是( )
,则由这两平面所成的二面角的正弦值是( )
A.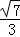 B.
B.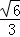 C.
C.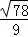 D.
D.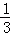
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
(2012•静安区一模)在棱长为1的正方体ABCD﹣A1B1C1D1中,E为棱BC的中点,F为棱DD1的中点.则异面直线EF与BD1所成角的余弦值是( )
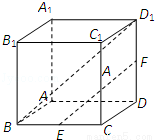
A.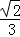 B.
B.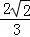 C.
C.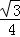 D.
D.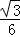
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:解答题
(本小题满分12分)口袋中装有除编号外其余完全相同的5个小球,编号依次为1,2,3,4,5.现从中同时取出两个球,分别记录下其编号为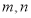 .
.
(Ⅰ)求“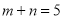 ”的概率;
”的概率;
(Ⅱ)求“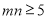 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:解答题
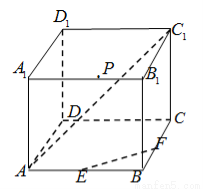
(本题满分12分)在长方体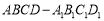 中,
中,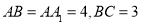 ,
,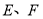 分别是所在棱
分别是所在棱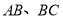 的中点,点
的中点,点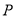 是棱
是棱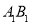 上的动点,联结
上的动点,联结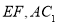 .如图所示.
.如图所示.
(1)求异面直线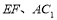 所成角的大小(用反三角函数值表示);
所成角的大小(用反三角函数值表示);
(2)求以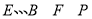 为顶点的三棱锥的体积.
为顶点的三棱锥的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com