
(2012•赣州模拟)函数f(x)=ax3+bx2+cx+d(a≠0),若a+b+c=0,导函数f′(x)满足f′(0)f′(1)>0,设f′(x)=0的两根为x1,x2,则|x1﹣x2|的取值范围是( )
A.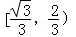 B.
B.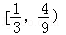 C.
C.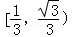 D.
D.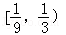
A
【解析】
试题分析:先求出f′(x)=3ax2+2bx+c,可得 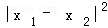 =
=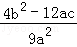 =
=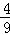
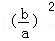 +
+ +
+ ,由f′0)•f′(1)>0,
,由f′0)•f′(1)>0,
解得﹣2<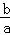 <﹣1,利用二次函数的性质求出
<﹣1,利用二次函数的性质求出 的范围,即可求得|x1﹣x2|的取值范围.
的范围,即可求得|x1﹣x2|的取值范围.
【解析】
由题意得:f′(x)=3ax2+2bx+c,∵x1,x2是方程f′(x)=0的两个根,
∴x1+x2=﹣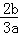 ,x1•x2=
,x1•x2=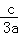 .∴|x1﹣x2|2 =
.∴|x1﹣x2|2 =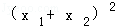 ﹣4x1x2 ,
﹣4x1x2 ,
∴ =
=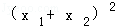 ﹣4x1•x2 =
﹣4x1•x2 = .
.
∵a+b+c=0,∴c=﹣a﹣b,
∴ =
=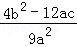 =
=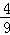
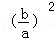 +
+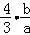 +
+ .
.
∵f′0)•f′(1)>0,f(0)=c=﹣(a+b),且f′(1)=3a+2b+c=2a+b,∴(a+b)(2a+b)<0,
即2a2+3ab+b2<0,∵a≠0,两边同除以a2得: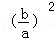 +3
+3 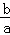 +2<0,解得﹣2<
+2<0,解得﹣2<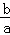 <﹣1.
<﹣1.
由二次函数的性质可得,当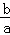 =﹣
=﹣ 时,
时,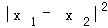 有最小值为
有最小值为 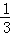 ,
,
当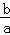 趋于﹣1时,
趋于﹣1时,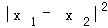 趋于
趋于 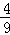 ,故
,故 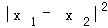 ∈
∈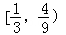 ,
,
故|x1﹣x2|∈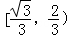 ,
,
故选A.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
如图,一个半径为1的球O放在桌面上,桌面上的一点A1的正上方有一光源A,AA1与球相切,AA1=3,球在桌面上的投影是一个椭圆C,记椭圆C的四个顶点分别为A1、A2、B1、B2.则对于下列的命题:
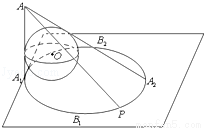
①若点P为椭圆C上的一个动点,则tan∠OAP=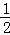 ;
;
②椭圆C的长轴长为4;
③若沿直线B1B2的方向为主视方向,则几何体A﹣A1B1A2B2的左视图的面积为3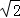 ;
;
④椭圆C的离心率为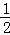
其中真命题的序号为 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
曲线f(x)=lnx+2x在点(1,f(1))处的切线方程是( )
A.3x﹣y+1=0 B.3x﹣y﹣1=0 C.3x+y﹣1=0 D.3x﹣y﹣5=0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
若f(x)=sinx+cosx,则 等于( )
等于( )
A.﹣1 B.0 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2014•上海二模)已知f(x)=(2x+1)3﹣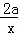 +3a,若f′(﹣1)=8,则f(﹣1)=( )
+3a,若f′(﹣1)=8,则f(﹣1)=( )
A.4 B.5 C.﹣2 D.﹣3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
ABCD是正方形,PA⊥平面AC,且PA=AB,则二面角B﹣PC﹣D的度数为( )
A.60° B.90° C.120° D.135°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:选择题
已知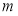 ,
,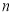 是两条不同直线,
是两条不同直线,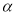 ,
,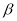 是两个不同的平面,且
是两个不同的平面,且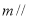
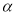 ,
,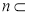
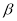 ,则下列叙述正确的是( )
,则下列叙述正确的是( )
(A)若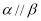 ,则
,则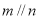
(B)若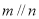 ,则
,则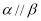
(C)若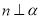 ,则
,则
(D)若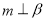 ,则
,则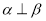
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com