
如图,一个半径为1的球O放在桌面上,桌面上的一点A1的正上方有一光源A,AA1与球相切,AA1=3,球在桌面上的投影是一个椭圆C,记椭圆C的四个顶点分别为A1、A2、B1、B2.则对于下列的命题:
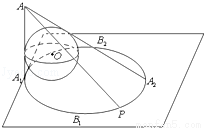
①若点P为椭圆C上的一个动点,则tan∠OAP=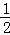 ;
;
②椭圆C的长轴长为4;
③若沿直线B1B2的方向为主视方向,则几何体A﹣A1B1A2B2的左视图的面积为3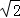 ;
;
④椭圆C的离心率为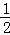
其中真命题的序号为 .(写出所有真命题的序号)
①②④
【解析】
试题分析:根据题意作出过圆锥的轴与椭圆长轴AA1的截面,根据圆锥曲线的定义,可得球与长轴A1A2的切点是椭圆的焦点F,运用切线长定理,求出AE,AD,即可判断①;②由二倍角的正切公式,以及正切函数的定义,即可得到长轴长;求出a,c,b,即可得到几何体A﹣A1B1A2B2的左视图的面积为 ×3×2
×3×2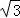 =3
=3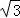 ,即可判断③;由椭圆的离心率公式,即可判断④.
,即可判断③;由椭圆的离心率公式,即可判断④.
解如图是过锥体的轴与椭圆长轴A1A2的截面,根据圆锥曲线的定义,
可得球与长轴A1A2的切点是椭圆的焦点F,OE=OF=1,A1E=A1F=1,AA1=3,
AE=2,AD=2,
对于①,tan∠OAP=tan∠OAD=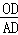 =
= ,故①对;
,故①对;
对于②,tan∠A1AA2=tan2∠OAD=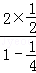 =
=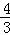 ,
,
A1A2=AA1•tan∠A1AA2=3×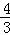 =4,故②对;
=4,故②对;
对于③由于2a=4,a=2,a﹣c=1,c=1,b2=a2﹣c2=3,b=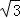 ,
,
若沿直线B1B2的方向为主视方向,则几何体A﹣A1B1A2B2的左视图的面积为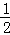 ×3×2
×3×2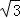 =3
=3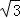 ,故③错;
,故③错;
对于④椭圆C的离心率为e=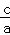 =
= ,故④对.
,故④对.
故答案为:①②④.


科目:高中数学 来源:2014-2015学年天津市高三上学期第二次月考文科数学试卷(解析版) 题型:选择题
定义一种运算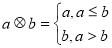 ,令
,令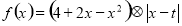 (
(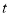 为常数),且
为常数),且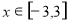 ,则使函数
,则使函数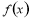 最大值为4的
最大值为4的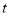 值是( )
值是( )
A.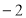 或
或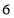 B.
B.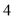 或
或 C.
C.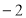 或
或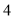 D.
D.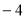 或
或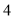
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:填空题
把数列 的所有数按照从大到小的原则写成如下数表:
的所有数按照从大到小的原则写成如下数表:
1
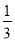


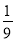
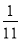









第 行有
行有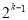 个数,第
个数,第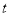 行的第
行的第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:选择题
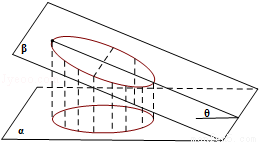
(2014•安徽模拟)如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )
A.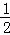 B.
B.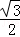 C.
C.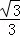 D.
D.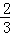
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
(2011•南充模拟)在60°的二面角内放入一个球,球与该二面角的两个半平面分别切于两点A,B,且A、B两点的球面距离为2πcm,则该球的半径为 cm..
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2009•四川)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
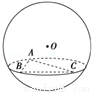
A.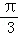 B.π C.
B.π C.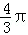 D.2π
D.2π
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2012•赣州模拟)函数f(x)=ax3+bx2+cx+d(a≠0),若a+b+c=0,导函数f′(x)满足f′(0)f′(1)>0,设f′(x)=0的两根为x1,x2,则|x1﹣x2|的取值范围是( )
A.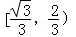 B.
B.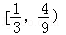 C.
C.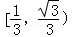 D.
D.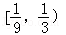
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com