练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知超几何分布满足X～H（8，5，3），则P（X=2）= ．

    【解析】

    试题分析：根据超几何分布得N=8，M=5，n=2，由超几何概率计算公式可得．

    【解析】
    ∵超几何分布满足X～H（8，5，3），

    ∴P（X=2）=C=．

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014-2015学年贵州省高三模拟考试文科数学试卷（解析版） 题型：选择题

    的值为

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系（解析版） 题型：填空题

    如图，一个半径为1的球O放在桌面上，桌面上的一点A1的正上方有一光源A，AA1与球相切，AA1=3，球在桌面上的投影是一个椭圆C，记椭圆C的四个顶点分别为A1、A2、B1、B2．则对于下列的命题：

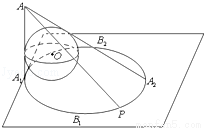
    ①若点P为椭圆C上的一个动点，则tan∠OAP=；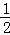

    ②椭圆C的长轴长为4；

    ③若沿直线B1B2的方向为主视方向，则几何体A﹣A1B1A2B2的左视图的面积为3；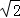

    ④椭圆C的离心率为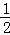

    其中真命题的序号为 ．（写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-3 2.2超几何分布练习卷（解析版） 题型：解答题

    生产方提供50箱的一批产品，其中有2箱不合格产品．采购方接收该批产品的准则是：从该批产品中任取5箱产品进行检测，若至多有1箱不合格产品，便接收该批产品．问：该批产品被接收的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-3 2.2超几何分布练习卷（解析版） 题型：解答题

    已知10件不同的产品中共有3件次品，现对它们进行一一测试，直到找出所有3件次品为止．

    （1）求恰好在第5次测试时3件次品全部被测出的概率；

    （2）记恰好在第k次测试时3件次品全部被测出的概率为f（k），求f（k）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-3 2.2超几何分布练习卷（解析版） 题型：解答题

    电子手表厂生产某批电子手表正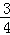品率为，次品率为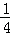，现对该批电子手表进行测试，设第X次首次测到正品，则P（1≤X≤2013）等于（ ）

    A.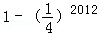

    B.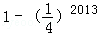

    C.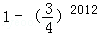

    D.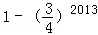

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷（解析版） 题型：?????

    曲线f（x）=lnx+2x在点（1，f（1））处的切线方程是（ ）

    A.3x﹣y+1=0 B.3x﹣y﹣1=0 C.3x+y﹣1=0 D.3x﹣y﹣5=0

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷（解析版） 题型：?????

    若f（x）=sinx+cosx，则等于（ ）

    A.﹣1 B.0 C.1 D.2

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷（解析版） 题型：填空题

    若，，则= ．

    查看答案和解析>>

    同步练习册答案