
生产方提供50箱的一批产品,其中有2箱不合格产品.采购方接收该批产品的准则是:从该批产品中任取5箱产品进行检测,若至多有1箱不合格产品,便接收该批产品.问:该批产品被接收的概率是多少?
 习题精选系列答案
习题精选系列答案科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:填空题
给出两个函数性质:
性质1: 是偶函数;
是偶函数;
性质2: 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
对于函数:① ;②
;② ; ③
; ③ ,
,
上述两个函数性质都具有的所有函数的序号是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
(2011•南充模拟)在60°的二面角内放入一个球,球与该二面角的两个半平面分别切于两点A,B,且A、B两点的球面距离为2πcm,则该球的半径为 cm..
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2009•四川)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
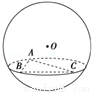
A.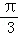 B.π C.
B.π C.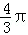 D.2π
D.2π
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某热水瓶胆生产的6件产品中,有4件正品,2件次品,正品和次品在外观上没有区别,从这6件产品中任意抽检2件,计算
(1)2件都是正品的概率
(2)至少有一件次品的概率.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
已知y=f(x)=ln|x|,则下列各命题中,正确的命题是( )
A.x>0时,f′(x)= ,x<0时,f′(x)=﹣
,x<0时,f′(x)=﹣
B.x>0时,f′(x)= ,x<0时,f′(x)无意义
,x<0时,f′(x)无意义
C.x≠0时,都有f′(x)=
D.∵x=0时f(x)无意义,∴对y=ln|x|不能求导
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
在空间中,“经过点P(x0,y0,z0),法向量为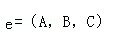 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是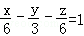 ,则由这两平面所成的二面角的正弦值是( )
,则由这两平面所成的二面角的正弦值是( )
A.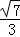 B.
B.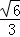 C.
C.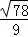 D.
D.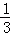
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com