
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为f(k),求f(k)的最大值和最小值.
(1)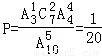
(2)故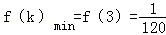 ,
,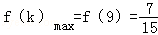 .
.
【解析】
试题分析:(1)根据题意,若恰好在第5次测试时3件次品全部被测出,则第5次取出第3件次品,前4次中有2次是次品,2次是正品;有排列、组合数公式可得其情况数目,易得从10件产品中顺序取出5件的情况数目,由等可能事件的概率,计算可得答案;
(2)根据题意,分析可得k的范围是3≤k≤9,进而分3≤k≤6、7≤k≤9时讨论,由等可能事件计算可得f(k),比较大小可得答案.
【解析】
(1)若恰好在第5次测试时3件次品全部被测出,则第5次取出第3件次品,前4次中有2次是次品,2次是正品;
则有A31C72A44种情况,从10件产品中顺序取出5件,有A105种情况,
则第5次测试时3件次品全部被测出的概率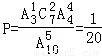 ,
,
(2)根据题意,分析可得k的范围是3≤k≤9,
当3≤k≤6时,若恰好在第k次测试时3件次品全部被测出,则第k次取出第3件次品,前k﹣1次中有2次是次品,k﹣3次是正品;而从10件产品中顺序取出k件,有A10k种情况,则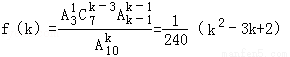 ,
,
则f(3)=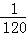 ,f(4)=
,f(4)= ,f(5)=
,f(5)=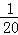 ,f(6)=
,f(6)=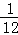 ;
;
当k=7时,即恰好在第7次测试时3件次品全部被测出,有两种情况,一是第7次取出第3件次品,前6次中有2次是次品,4次是正品;二是前7次没有取出次品,此时也可以测出三件次品,
则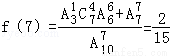 ;
;
当k=8时,即恰好在第7次测试时3件次品全部被测出,有两种情况,一是第8次取出第3件次品,前7次中有2次是次品,5次是正品;二是前7次恰有一次次品,第8次取出为合格品,
则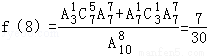 ;
;
当k=9时,即恰好在第9次测试时3件次品全部被测出,有两种情况,一是第9次取出第3件次品,前8次中有2次是次品,6次是正品;二是前8次取出1次次品,第9次取出第2件次品,
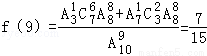 .
.
故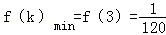 ,
,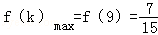 .
.


科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:选择题
将函数 的图像向右平移
的图像向右平移 个单位,再向上平移
个单位,再向上平移 个单位,
个单位,
所得函数图像对应的解析式为
A.
B.
C.
D.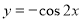
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:选择题
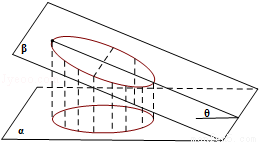
(2014•安徽模拟)如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )
A.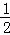 B.
B.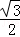 C.
C.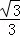 D.
D.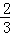
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2009•四川)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
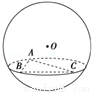
A.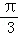 B.π C.
B.π C.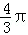 D.2π
D.2π
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某批产品共10件,已知从该批产品中任取1件,则取到的是次品的概率为P=0.2.若从该批产品中任意抽取3件,
(1)求取出的3件产品中恰好有一件次品的概率;
(2)求取出的3件产品中次品的件数X的概率分布列与期望.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
若函数f(x)=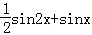 ,则f′(x)是( )
,则f′(x)是( )
A.仅有最小值的奇函数
B.仅有最大值的偶函数
C.既有最大值又有最小值的偶函数
D.非奇非偶函数
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
(2012•德阳三模)已知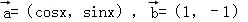 ,将函数
,将函数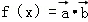 的图象按向量
的图象按向量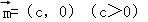 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
A.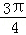 B.π C.
B.π C.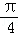 D.
D.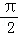
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
(2012•静安区一模)在棱长为1的正方体ABCD﹣A1B1C1D1中,E为棱BC的中点,F为棱DD1的中点.则异面直线EF与BD1所成角的余弦值是( )
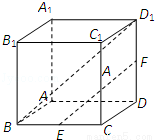
A.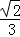 B.
B.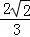 C.
C.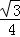 D.
D.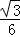
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com