
 某三棱锥的三视图如图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$.
某三棱锥的三视图如图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$. 分析 根据几何体的三视图得出该三棱锥的侧面垂直于底面,求出四个面的面积即可得出结论.
解答 解:根据三视图得,该三棱锥的直观图如图所示,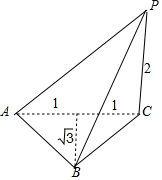
该三棱锥中,侧面PAC⊥底面ABC,
S△ABC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
S△PAC=$\frac{1}{2}$×2×2=2,
S△PBC=$\frac{1}{2}$×2×$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2,
S△PAB=$\frac{1}{2}$×2×$\sqrt{{2}^{2}{+2}^{2}{-(\frac{2}{2})}^{2}}$=$\sqrt{7}$;
三棱锥的四个面中,面积最大的面PAB的面积是$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题主要考查了三视图的识别和应用问题,根据三视图确定三棱锥的各面面积是解题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
下面用茎叶图记录了同班的甲、乙两名学生4次数学考试成绩,其中甲的一次成绩模糊不清,用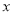 标记.
标记.
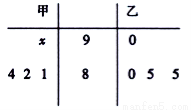
(1)求甲生成绩的中位数与乙生成绩的众数;
(2)若甲、乙这4次的平均成绩相同,确定甲、乙中谁的成绩更稳定,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.852 | B. | 0.8192 | C. | 0.8 | D. | 0.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时有
时有 .
.
①求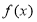 的解析式;
的解析式;
②求 的值域;
的值域;
③若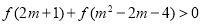 ,求
,求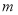 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
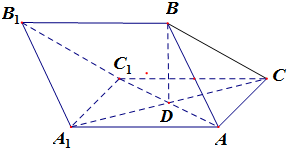 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com