
分析 (1)由向量的数量积运算,二倍角公式及变形、两角和的正弦公式化简解析式,由正弦函数的对称轴求出函数f(x)的对称轴方程;
(2)由(1)求出函数的周期性,由正弦函数的图象画出f(x)的图象,根据题意和图象对t分类讨论,由正弦函数的性质分别求出函数f(x)的最值,以及g(t)的解析式;
(3)由题意可得函数H(x)=x|x-k|+2k-8在[4,+∞)上的值域是h(x)在[4,+∞)上的值域的子集,分类讨论求得k的范围.
解答 解:(1)∵向量$\overrightarrow{a}$=($\sqrt{2}$sin($\frac{π}{4}$x-$\frac{π}{8}$),cos2($\frac{π}{4}$x-$\frac{π}{8}$)-$\frac{1}{2}$),$\overrightarrow{b}$=(cos($\frac{π}{4}$x-$\frac{π}{8}$),$\sqrt{2}$),
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{2}$sin($\frac{π}{4}$x-$\frac{π}{8}$)cos($\frac{π}{4}$x-$\frac{π}{8}$)+$\sqrt{2}$cos2($\frac{π}{4}$x-$\frac{π}{8}$)
=$\frac{\sqrt{2}}{2}sin(\frac{π}{2}x-\frac{π}{4})$+$\frac{\sqrt{2}}{2}$[1+cos($\frac{π}{2}x-\frac{π}{4}$)]=$sin\frac{π}{2}x+\frac{\sqrt{2}}{2}$,
由$\frac{π}{2}x=\frac{π}{2}+kπ(k∈Z)$得,x=1+2k(k∈Z)
∴函数f(x)的对称轴方程是x=1+2k(k∈Z);
(2)由(1)得,f(x)=$sin\frac{π}{2}x+\frac{\sqrt{2}}{2}$,最小正周期是4,
由t∈[-2,0]得,t+1∈[-1,1],
画出函数f(x)的部分图象,如右图,
当-2≤t<-$\frac{3}{2}$,时,f(x)在区间[t,t+1]上,
最小值为m(t)=$-1+\frac{\sqrt{2}}{2}$,
最大值为M(t)=f(t)=sin$\frac{πt}{2}$+$\frac{\sqrt{2}}{2}$,
∴g(t)=M(t)-m(t)=1+sin$\frac{πt}{2}$;
当-$\frac{3}{2}$≤t<-1时,f(x)在区间[t,t+1]上的最小值为m(t)=-1+$\frac{\sqrt{2}}{2}$,
最大值为M(t)=f(t+1)=sin$\frac{πt+π}{2}$+$\frac{\sqrt{2}}{2}$=cos$\frac{πt}{2}$+$\frac{\sqrt{2}}{2}$,
∴g(t)=M(t)-m(t)=1+cos$\frac{πt}{2}$,
当-1≤t≤0时,在区间[t,t+1]上,最小值为m(t)=f(t)=sin$\frac{πt}{2}$+$\frac{\sqrt{2}}{2}$,
最大值为M(t)=f(t+1)=sin$\frac{πt+π}{2}$+$\frac{\sqrt{2}}{2}$=cos$\frac{πt}{2}$+$\frac{\sqrt{2}}{2}$,
∴g(t)=M(t)-m(t)=cos$\frac{πt}{2}$-sin$\frac{πt}{2}$=$\sqrt{2}cos(\frac{πt}{2}+\frac{π}{4})$,
综上可得,g(t)=$\left\{\begin{array}{l}{1+sin\frac{πt}{2},-2≤t<-\frac{3}{2}}\\{1+cos\frac{πt}{2},-\frac{3}{2}≤t<-1}\\{\sqrt{2}cos(\frac{πt}{2}+\frac{π}{4}),-≤t≤0}\end{array}\right.$;
(3)函数f(x)=sin$\frac{πt}{2}$+$\frac{\sqrt{2}}{2}$的最小正周期为4,
∴M(t+4)=M(t),m(t+4)=m(t).
函数h(x)=2|x-k|,H(x)=x|x-k|+2k-8,
对任意x1∈[4,+∞),存在x2∈(-∞,4],使得h(x2)=H(x1)成立,
即函数H(x)=x|x-k|+2k-8在[4,+∞)上的值域是h(x)在[4,+∞)上的值域的子集.
∵h(x)=|2|x-k|=$\left\{\begin{array}{l}{{2}^{x-k},x≥k}\\{{2}^{k-x},x<k}\end{array}\right.$,
①当k≤4时,h(x)在(-∞,k)上单调递减,在[k,4]上单调递增.
故h(x)的最小值为h(k)=1;
∵H(x)在[4,+∞)上单调递增,故H(x)的最小值为H(4)=8-2k.
由8-2k≥1,求得k≤$\frac{7}{2}$.
②当4<k≤5时,h(x)在(-∞,4]上单调递减,h(x)的最小值为h(4)=2k-4,
H(x)在[k,4]上单调递减,在(k,+∞)上单调递增,
故H(x)的最小值为H(k)=2k-8,由$\left\{\begin{array}{l}{4<k≤5}\\{2k-8≥{2}^{k-4}}\end{array}\right.$得,k=5,
综上可得,k的范围为(-∞,$\frac{7}{2}$]∪{5}.
点评 本题考查向量的数量积运算,三角恒等变换中的公式,正弦函数的图象与性质,指数函数的图象特征,函数的能成立、函数的恒成立问题,考查分类讨论思想,数形结合思想,化简、变形能力,属于难题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{7}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n | B. | $\frac{1}{3}$×2n-2 | C. | -$\frac{1}{3}$×2n-2 | D. | 3×2n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
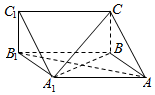 如图,在三棱柱ABC-A1B1C1中,A1A=AB,CB⊥A1ABB1.
如图,在三棱柱ABC-A1B1C1中,A1A=AB,CB⊥A1ABB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com