
| A. | ($\frac{\sqrt{6}}{3}$,1) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
分析 根据题意设P(bsinα,acosα),求出${k}_{P{A}_{1}}$,${k}_{P{A}_{2}}$,结合${k}_{P{A}_{1}}$•${k}_{P{A}_{2}}$>-3及隐含条件列式求得椭圆离心率的取值范围.
解答 解:设P(bsinα,acosα),A1(0,-a),A2(0,a).
∴${k}_{P{A}_{1}}=\frac{acosα+a}{bsinα},{k}_{P{A}_{2}}=\frac{acosα-a}{bsinα}$,
由${k}_{P{A}_{1}}$•${k}_{P{A}_{2}}$>-3,得$\frac{{a}^{2}(co{s}^{2}α-1)}{{b}^{2}si{n}^{2}α}$>-3,
即$-\frac{{a}^{2}si{n}^{2}α}{{b}^{2}si{n}^{2}α}>-3$,∴$\frac{{a}^{2}}{{b}^{2}}<3$,
则a2<3(a2-c2),∴2a2>3c2,
得$\frac{{c}^{2}}{{a}^{2}}<\frac{2}{3}$,即e∈(0,$\frac{\sqrt{6}}{3}$),
故选:B.
点评 本题考查椭圆的简单性质,考查由两点坐标求斜率公式,正确设出p的坐标是求解本题的关键,是中档题.


科目:高中数学 来源: 题型:解答题
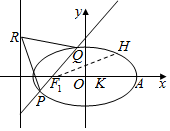 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+2)2+(y+1)2=5 | B. | (x-2)2+(y-1)2=10 | C. | (x-2)2+(y-1)2=5 | D. | (x+2)2+(y+1)2=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {(0,2)} | C. | {2} | D. | {(2,0)} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com