
| A. | $\frac{{x}^{2}}{3}$-$\frac{8{y}^{2}}{25}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{6}$-$\frac{2{y}^{2}}{25}$=1 | D. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{50}$=1 |
分析 利用圆心G到原点O的距离为$\sqrt{5}$,求出a,利用等面积,结合双曲线的定义,求出P的坐标,即可得出结论.
解答 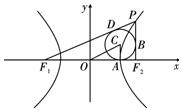 解:设圆与F1F2,PF1,PF2的切点分别为A,B,D.则OA=a,
解:设圆与F1F2,PF1,PF2的切点分别为A,B,D.则OA=a,
故$\sqrt{{a}^{2}+1}$=$\sqrt{5}$,即a=2.
又△PF1F2的面积S=$\frac{1}{2}×2c×\frac{5}{2}$=$\frac{1}{2}$(|F1F2|+|PF1|+|PF2|×1,
∴|PF1|+|PF2|=3c,
∵|PF1|-|PF2|=2a,
∴|PF1|=$\frac{3c+2a}{2}$,|PF2|=$\frac{3c-2a}{2}$,
∵|PF1|=$\sqrt{({x}_{0}+c)^{2}+\frac{25}{4}}$,|PF2|=$\sqrt{({x}_{0}-c)^{2}+\frac{25}{4}}$,联立化简得x0=3.
P代入双曲线方程,联立解得b=$\sqrt{5}$,
即有双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1.
故选B.
点评 本题考查双曲线的方程与性质,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{3},2}]$ | B. | $[{1,\frac{8}{3}})$ | C. | $[{2,\frac{8}{3}})$ | D. | $({-∞,\frac{8}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
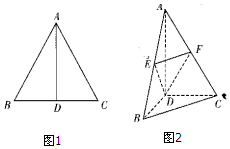 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄ξ服从正态分布N(μ,σ2),同时随机抽取100位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分别区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.
京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄ξ服从正态分布N(μ,σ2),同时随机抽取100位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分别区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com