练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知等比数列{an}中，a2a4=a5，a4=8，则公比q=2，其前4项和S4=15．

    分析 设等比数列{an}的公比为q，由a2a4=a5，a4=8，可得${a}_{2}^{2}$q2=a2q3，${a}_{2}{q}^{2}$=8，解得a2，q，利用求和公式即可得出．

    解答 解：设等比数列{an}的公比为q，∵a2a4=a5，a4=8，
    ∴${a}_{2}^{2}$q2=a2q3，${a}_{2}{q}^{2}$=8，解得a2=q=2．
    ∴a1=1．
    其前4项和S4=$\frac{1×（{2}^{4}-1）}{2-1}$=15．
    故答案为：2，15．

    点评 本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．（3a+2b）6的展开式中的第3项的二项式系数为15．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知在平面直角坐标系中，曲线C1的参数方程是$\left\{\begin{array}{l}x=-1+cosθ\\ y=sinθ\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程是ρ=2sinθ．
    （Ⅰ） 求曲线C1与C2交点的平面直角坐标；
    （Ⅱ） 点A，B分别在曲线C1，C2上，当|AB|最大时，求△OAB的面积（O为坐标原点）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．等比数列{an}中各项均为正数，Sn是其前n项和，且满足2S3=8a1+3a2，a4=16，则S4=（　　）
    A．9B．15C．18D．30

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．圆心为（0，1）且与直线y=2相切的圆的方程为（　　）
    A．（x-1）2+y2=1B．（x+1）2+y2=1C．x2+（y-1）2=1D．x2+（y+1）2=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．某地区以“绿色出行”为宗旨开展“共享单车”业务．该地有a，b两种“共享单车”（以下简称a型车，b型车）．某学习小组7名同学调查了该地区共享单车的使用情况．
    （Ⅰ）某日该学习小组进行一次市场体验，其中4人租到a型车，3人租到b型车．如果从组内随机抽取2人，求抽取的2人中至少有一人在市场体验过程中租到a型车的概率；
    （Ⅱ）根据已公布的2016年该地区全年市场调查报告，小组同学发现3月，4月的用户租车情况城现如表使用规律．例如，第3个月租a型车的用户中，在第4个月有60%的用户仍租a型车．

    第3个月
    第4个月    		租用a型车租用b型车
    租用a型车60%50%
    租用b型车40%50%
    若认为2017年该地区租用单车情况与2016年大致相同．已知2017年3月该地区租用a，b两种车型的用户比例为1：1，根据表格提供的信息，估计2017年4月该地区租用两种车型的用户比例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．数列{an}中，已知a1=1，a2=a，an+1=k（an+an+2）对任意n∈N*都成立，数列{an}的前n项和为Sn．（这里a，k均为实数）
    （1）若{an}是等差数列，求Sn；
    （2）若a=1，k=-$\frac{1}{2}$，求Sn；
    （3）是否存在实数k，使数列{an}是公比不为1的等比数列，且任意相邻三项am，am+1，am+2按某顺序排列后成等差数列？若存在，求出所有k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

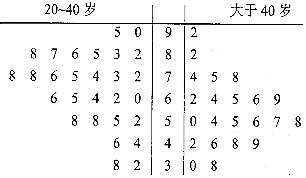    17．某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示．
    （1）根据茎叶图中的数据完成2×2列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
    购买意愿强购买意愿弱合计
    20-40岁
    大于40岁
    合计
    （2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，记抽到的2人中年龄大于40岁的市民人数为X，求X的分布列和数学期望．
    附：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
    P（K2≥k0）0.1000.0500.0100.001
    k02.7063.8416.63510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，点P（x0，$\frac{5}{2}$）为双曲线上一点，若△PF1F2的内切圆半径为1，且圆心G到原点O的距离为$\sqrt{5}$，则双曲线的方程为（　　）
    A．$\frac{{x}^{2}}{3}$-$\frac{8{y}^{2}}{25}$=1B．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1C．$\frac{{x}^{2}}{6}$-$\frac{2{y}^{2}}{25}$=1D．$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{50}$=1

    查看答案和解析>>

    同步练习册答案